Question

ABCD is a rhombus, EABF is a straight line such that EA = AB = BF. Prove that ED and FC when produced meet at right angles.

Answer 1

Hint: For solving this problem, we first produce a diagram for simplification and better understanding. Now, by using the reference of the diagram we apply some properties of rhombus to obtain the desired result.

Complete Step-by-Step solution:

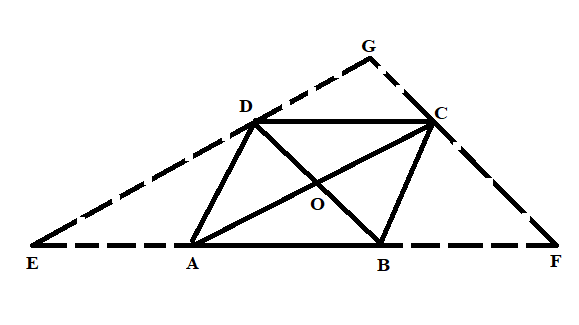
Given: ABCE is a rhombus, EABF is a straight line such that EA = AB =BF.
To prove: ED and FC when produced meet at right angles.
Proof: Using the theorem “The diagonals of a rhombus are perpendicular bisector of each other”. So, from this theorem, we concluded that
$OA=OC,OB=OD,\angle AOD=\angle COD={{90}^{\circ \text{ }}}and\text{ }\angle \text{COB=9}{{\text{0}}^{\circ \text{ }}}$
Now, consider the $\Delta BDE$, from the above figure it is clear that A and O are the mid points of the BE and BD respectively. Therefore, we obtain that OA is parallel to DE and OC is parallel to DG.
Now, consider the $\Delta CFA$, from the above figure it is clear that B and O are the mid points of the AF and AC respectively. Therefore, we obtain that OB is parallel to CF and OD is parallel to GC.
Thus, we concluded that in quadrilateral GOCD, OC is parallel to DG and OD is parallel to GC.
So, the GOCD is the parallelogram.
Therefore, by using the property of parallelogram, $\angle DGC=\angle DOC$.
Since, $\angle DCG={{90}^{\circ }}$ because of rhombus property of perpendicular bisectors.
Hence, we proved that the ED and FC when produced meet at right angles.

Note: The key step for solving this problem is the knowledge of geometrical figures, particularly rhombus. By using the properties of rhombus, the desired result is obtained without error. This problem enhances the observational qualities of a student.