Question

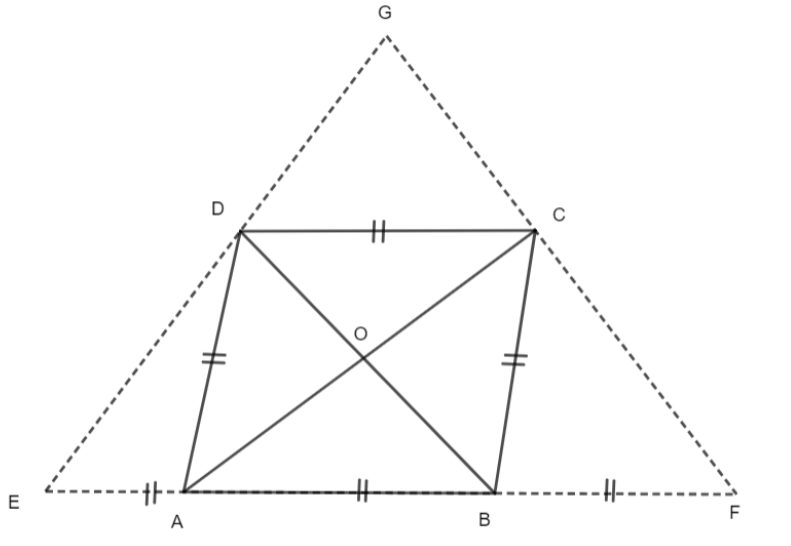
ABCD is a rhombus. EAB is a straight line such that AB = EA = BF. Prove that ED and FC when produced meet at right angles.

Answer 1

Hint: To solve this question, we will separately consider triangles BDE and CFA and then apply the midpoint theorem of the triangle in them to get the two parallel sides. By getting these two pairs of parallel sides, we will prove that DOCG to be a parallelogram. Finally, we will use that opposite angles of a parallelogram are equal to get the answer. Also, the midpoint theorem is stated as “The line segment connecting the midpoints of two sides of a triangle is parallel to the third side and is congruent to one half of the third side.”

Complete step-by-step solution
We are given a Rhombus ABCD and all sides are equal.
\[AB=CD=BC=AD.......\left( i \right)\]
Now, we are also given that EABF is a straight line and
\[AB=EA=BF......\left( ii \right)\]
From equations (i) and (ii), we have that \[AB=BC=CD=DA=EA=BF\] are equal.
Now, let us draw the figure.

Now because the diagonals of a rhombus are perpendicular bisectors of each other.
\[\Rightarrow \angle AOD=\angle COD={{90}^{\circ }}\]
Also, for the same reason, \[\angle AOB=\angle COB={{90}^{\circ }}.\]
Now, let us consider triangle BDE, because AE = AB, A is the midpoint of line EB and also as diagonals of the rhombus are perpendicular bisector,
\[OD=OB\]
From this, O is the midpoint of BD.
In triangle BDE, A and O are the midpoints of BE and BD respectively.
Now, we have the midpoint theorem stated as “The line segment connecting the midpoints of two sides of a triangle is parallel to the third side and is congruent to one half of the third side.” Applying this midpoint theorem in triangle BDE, we get as A and O are the midpoints of BE and BD respectively.
\[\Rightarrow OA||DE\]
\[\Rightarrow OC||DG\]
As all are the same line.
Similarly, consider triangle CFA, because AB = BF and B is the midpoint of AF. Also, DO = OB, and O is the midpoint of AC.
In triangle CFA, B and O are the midpoints of AF and AC respectively. Similarly, as done above by applying the midpoint theorem stated above, here we get, OB||CF and OD||GC.
Thus in equilateral DOCG, we have, OC||DG and OD||GC.
Now because the opposite sides are parallel, DOCG is a parallelogram. Again because the opposite angles of a parallelogram are equal,
\[\Rightarrow \angle DGC=\angle DOC\]
And the measure of \[\angle DOC={{90}^{\circ }}\] as the diagonal of a rhombus bisects at 90 degrees.
\[\Rightarrow \angle DGC=\angle DOC={{90}^{\circ }}\]
\[\Rightarrow \angle DGC={{90}^{\circ }}\]
Hence, we have proved that ED and FC when produced meet at right angles.

Note: A key point to note here in this question is that even though we only took OC||DG and OD||GC and not the opposite sides equal, then also the quadrilateral DOCG is a parallelogram. This is because we already had all the sides as equal.