Question

ABCD is a rhombus. Angle BDC $=27{}^\circ $ . The diagonals AC and BD cross at O. Calculate the size of angle ADC.

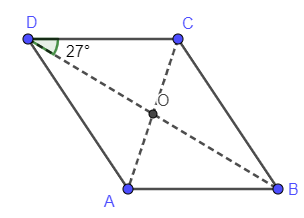
Answer 1

Hint: Firstly, apply the properties of rhombus to the angle at a given vertex. So, by that you can say the total angle made at vertex from the rule of adjacent angles are supplementary, find the angle which is required in the question.

Complete step-by-step answer:
Rule-1: Diagonals bisect each other. Thereby, bisect the angle at vertex.

Rule-1: Adjacent angles are supplementary.

Proof of diagonals bisect the angles:

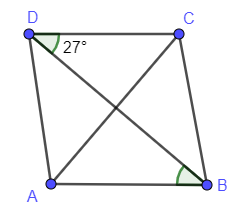
By definition, we know rhombus is a parallelogram. So, we take properties of parallel lines and their corresponding angles into consideration.
By figure we can say each diagonal divides the shape into 2 triangles. So, we can use the triangles congruence properties also.
You must also take the isosceles triangle and their properties into consideration.
We prove for the diagonal AC and we take BD granted as a similar way can be used for BD.

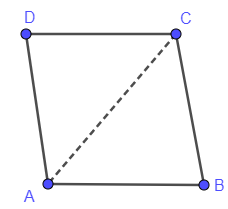
By saying the general condition in rhombus all sides are equal, we can say:

Line segment DA is congruent to line segment AB.

Line segment CD is congruent to line segment CB.

The line segment CA is the same in both. So, it is congruent to itself.

By SSS axiom, we say triangle CAD and triangle BAC are congruent. By this we can say angles BAC and CAD are congruent.

Using this throughout question, we get

$\angle ADC=\angle ADB+\angle BDC$

$\angle BDC=\angle ADB$

By substituting value of the angle BDC, we get that:

$\angle ADC=2\cdot \angle BDC=2.27$

By simplifying the above, we get value of ADC to be:

$\angle ADC=54{}^\circ $

Therefore, the required value of the angle ADC is $54{}^\circ $.

Note: The proof of similar triangles is crucial. So, always find the corresponding sides properly or else it might lead to the wrong conclusion.