Question

ABCD is a rectangle. Taking AD as a diameter, a semicircle AXD is drawn which intersects the diagonal BD at X. If $AB = 12cm$, $AD = 9cm$, the values of BD and BX are
A.$BD = 21cm$ and $BX = 5.4cm$
B.$BD = 9.6cm$ and $BX = 15cm$
C.$BD = 15cm$ and $BX = 9.6cm$
D.$BD = 25cm$ and $BX = 5.5cm$

Answer 1

Hint: Here, in the given question, we are given that ABCD is a rectangle in which taking AD as a diameter, a semicircle AXD is drawn which intersects the diagonal BD at X and we need to find the value of BD and BX if $AB = 12cm$, $AD = 9cm$. We will first draw the figure using the information given in the question. After this, we will observe the figure and use Pythagoras and tangent-secant theorem to find the value of BD and BX.

Complete answer:
Let us first draw the figure using the information given in the question.

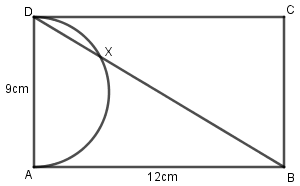
As we can see in the above-drawn figure that AB is a tangent (A line that touches the circle at a single point) to the circle with AD as diameter and DX is a secant (A secant of a circle is a line that intersects a circle at two distinct points) to the same circle. BD intersects the semi-circle at X.
Also, AB
$\angle DAB = 90^\circ $ since ABCD is a rectangle.
So, by Pythagoras theorem, we have
$B{D^2} = A{B^2} + A{D^2}$
$BD = \sqrt {A{B^2} + A{D^2}} $
Substitute the values of AB and AD.
$BD = \sqrt {{{12}^2} + {9^2}} $
$BD = \sqrt {144 + 81} $
On addition of terms, we get
$BD = \sqrt {225} $
$BD = 15cm$
Now we will apply the tangent-secant rule. According to the tangent-secant rule, if a secant and a tangent are drawn to a circle from the same external point, the product of the lengths of the secant and its external segment equals the square of the length of the tangent segment.
So now we have,
$ \Rightarrow BD \times BX = AB^2$
We can also write it as,
$ \Rightarrow BX = \dfrac{{A{B^2}}}{{BD}}$
On substituting the values, we get
$ \Rightarrow BX = \dfrac{{{{12}^2}}}{{15}}$
$ \Rightarrow BX = \dfrac{{144}}{{15}}$
On division, we get
$ \Rightarrow BX = 9.6cm$

Therefore, the correct option is C.

Note:
To solve these type of questions, one must first draw the figure using the information given in the question and observe the figure carefully. Use tangent-secant theorem carefully(According to tangent-secant rule, if a secant and a tangent are drawn to a circle from the same external point, the product of the lengths of the secant and its external segment equals the square of the length of the tangent segment). We should take care of the calculations so as to be sure of our final answer. Remember to write units.