Question

ABCD is a rectangle and P,Q, R and S are mid-points of the side AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.

Answer 1

Hint: Find out the length of each side of the rhombus using Pythagoras theorem. Hence, prove all the sides to be equal.

Complete step-by-step answer:
Given, ABCD is a rectangle.
P,Q, R and S are mid-points of AB, BC, CD and DA respectively.
To prove, PQRS is a rhombus.

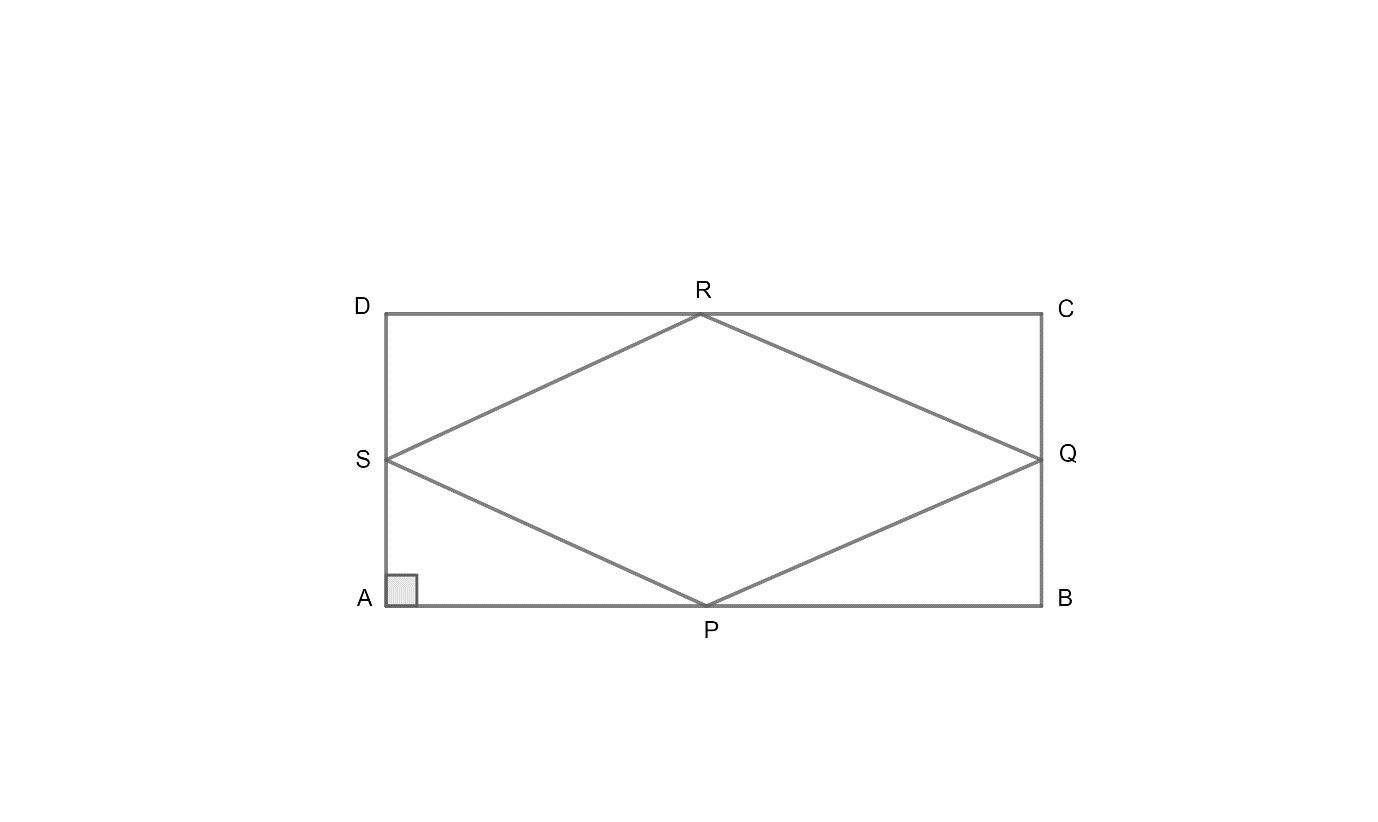
Let us assume, AB = CD = a and BC = AD = b.
$\Delta PQB$is a right angled triangle as $\angle B=90{}^\circ $. (Angles of a rectangle are $90{}^\circ $)
Applying the Pythagoras theorem on $\Delta PQB$, we get $P{{Q}^{2}}=B{{Q}^{2}}+B{{P}^{2}}$.
$BQ=\dfrac{BC}{2}=\dfrac{b}{2}$ as Q is the mid-point of BC.
$BP=\dfrac{AB}{2}=\dfrac{a}{2}$ as P is the mid-point of AB.
Putting the values of BP and BQ in $P{{Q}^{2}}=B{{Q}^{2}}+B{{P}^{2}}$, we get,
$\begin{align}
  & P{{Q}^{2}}=\dfrac{{{a}^{2}}}{4}+\dfrac{{{b}^{2}}}{4}=\dfrac{{{a}^{2}}+{{b}^{2}}}{4} \\
 & \Rightarrow PQ=\sqrt{\dfrac{{{a}^{2}}+{{b}^{2}}}{4}} \\
\end{align}$
Similarly, QR, RS and PS is equal to $\sqrt{\dfrac{{{a}^{2}}+{{b}^{2}}}{4}}$ as the triangles $\Delta BCR,\ \Delta RDC\ and\ \Delta SAP$are right angled triangles with sides $\dfrac{a}{2}\ and\ \dfrac{b}{2}$.
We can also clearly see that the angles made at each vertex are not equal to $90{}^\circ $.
Since all sides of quadrilateral PQRS are equal, it is a rhombus.


Note: (1) Opposite sides of the rectangle are equal.
(2) All angles of a rectangle are $90{}^\circ $.
(3) All sides of a rhombus are equal.
(4) In a right angled $\Delta ABC$, right angled at B,
$A{{B}^{2}}+A{{C}^{2}}=B{{C}^{2}}$.