Question

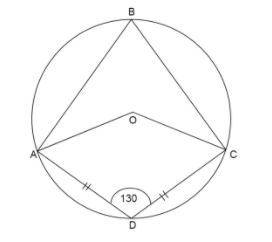
ABCD is a quadrilateral inscribed in a circle with center O, \[\angle ADC = {130^ \circ }\] and \[AD = DC\]. Calculate:
(i) reflex \[\angle AOC\]
(ii) \[\angle ABC\]
(iii) \[\angle AOD\]

Answer 1

Hint: Use the concept of cyclic quadrilateral and use the property of sum of opposite interior angles of a quadrilateral to calculate the value of \[\angle ABC\]. Use the angle subtended by the arc at center property to calculate the \[\angle AOC\]. Subtract this value from the whole angle \[{360^ \circ }\] to obtain the value of the reflex angle. For last part, construct OD which bisects \[\angle O\]
* A quadrilateral whose all 4 vertices lie on the circumference of a circle is called a cyclic quadrilateral. Sum of opposite interior angles in a cyclic quadrilateral is equal to \[{180^ \circ }\].
* Angle subtended by the arc of a circle at its center is twice the angle it subtends anywhere on the circumference.

Complete step-by-step solution:
We are given a quadrilateral ABCD is inscribed in a circle with center O.
Since all four vertices of quadrilateral ABCD lie on the circumference of the circle, the quadrilateral ABCD is a cyclic quadrilateral.
We know sum of opposite angles in quadrilateral is equal to \[{180^ \circ }\]
\[ \Rightarrow \angle ADC + \angle ABC = {180^ \circ }\]
Substitute the value of \[\angle ADC = {130^ \circ }\]
\[ \Rightarrow {130^ \circ } + \angle ABC = {180^ \circ }\]
Shift constant values to RHS of the equation
\[ \Rightarrow \angle ABC = {180^ \circ } - {130^ \circ }\]
\[ \Rightarrow \angle ABC = {50^ \circ }\]......................… (1)
Since we know angle subtended by arc of a circle at its center is twice the angle it subtends anywhere on the circumference, then \[\angle AOC = 2\angle ABC\]
\[ \Rightarrow \angle AOC = 2 \times {50^ \circ }\]
\[ \Rightarrow \angle AOC = {100^ \circ }\]....................… (2)
Then we know reflex angle \[\angle AOC = {360^ \circ } - {100^ \circ }\]
i.e. reflex angle \[\angle AOC = {260^ \circ }\].......................… (3)
Now we join OD which forms a radius of the circle.

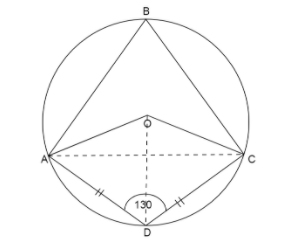
Since AOCD is a kite, then OD bisects \[\angle O\]
\[ \Rightarrow \angle AOD = \angle COD = \dfrac{{\angle AOC}}{2}\]
Substitute the value of \[\angle AOC = {260^ \circ }\]
\[ \Rightarrow \angle AOD = \angle COD = \dfrac{{{{260}^ \circ }}}{2}\]
\[ \Rightarrow \angle AOD = \angle COD = {130^ \circ }\]
\[ \Rightarrow \angle AOD = {130^ \circ }\]..................… (4)

\[\therefore \]The value of reflex angle \[\angle AOC = {260^ \circ }\], \[\angle ABC = {50^ \circ }\] and \[\angle AOD = {130^ \circ }\]

Note: Many students make mistakes in calculating the angle using the isosceles triangle property that radius forms two sides of the triangle so opposite angles must be equal, keep in mind we don’t have any value given for the triangle so we cannot find the value of equal angles. Also, this would require a lot of construction.