Question

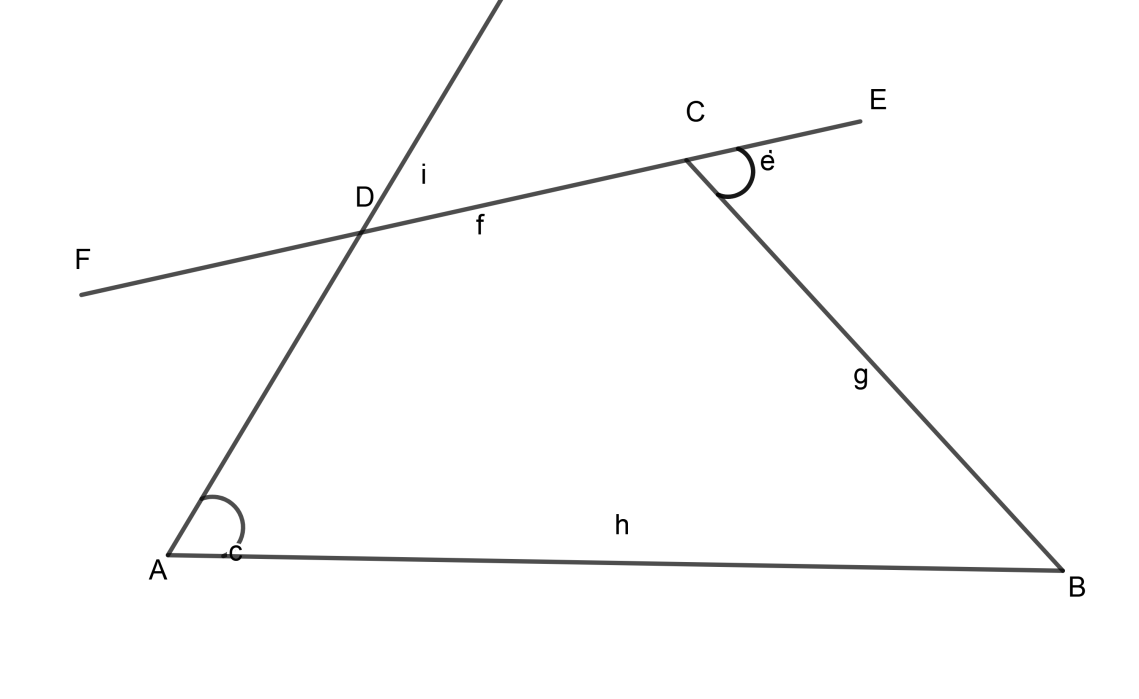
ABCD is a quadrilateral. If \[\angle A=\angle BCE\], is the quadrilateral a cyclic quadrilateral ? Give reasons.

Answer 1

Hint: To prove the above statement use the property of cyclic quadrilateral i. e. opposite angles of a cyclic quadrilateral are always Supplementary i.e. their summation is $180{}^\circ $.
Complete step-by-step answer:
To prove that quadrilateral ABCD is a cyclic quadrilateral, we should know the necessary and sufficient condition for a quadrilateral to be cyclic which is given below,
Concept: Opposite angles of a cyclic quadrilateral are always Supplementary i.e. their summation is $180{}^\circ $.
Which means we have to prove,
\[\angle A+\angle DCB=180{}^\circ and \angle ADC+\angle B=180{}^\circ \]
Let,
\[\angle A=\angle BCE=\theta \]……………………………….. (1)
From figure we can easily see that \[\angle DCE\] is a straight angle,
\[\therefore \angle DCE=180{}^\circ \]
But, from figure we can also write,
\[\angle DCE=\angle DCB+\angle ECB\]
Therefore from above two equations we can write,
\[\angle DCB+\angle ECB=180{}^\circ \]

Put the value of equation (1),
\[\therefore \angle DCB+\theta =180{}^\circ \]
\[\therefore \angle DCB=180{}^\circ -\theta \]…………………………………… (2)
Now we will add \[\angle Aand\angle DCB\] to see if they are supplementary.
\[\angle A+\angle DCB=\theta +\left( 180{}^\circ -\theta \right)\] [From (1) and (2)]
By giving separate signs in bracket we can write,
\[\therefore \angle A+\angle DCB=\theta +180{}^\circ -\theta \]
\[\therefore \angle A+\angle DCB=180{}^\circ \]……………………………………… (3)
Now, as we all know summation of all angles of a square is always \[360{}^\circ \],
\[\therefore \angle A+\angle B+\angle DCB+\angle ADC=360{}^\circ \]
By rearranging above equation,
\[\therefore \angle A+\angle DCB+\angle B+\angle ADC=360{}^\circ \]
Put the value of Equation (3) in above equation,
\[\therefore 180{}^\circ +\angle B+\angle ADC=360{}^\circ \]
\[\therefore \angle B+\angle ADC=360{}^\circ -180{}^\circ \]
\[\therefore \angle B+\angle ADC=180{}^\circ \]……………………………………….. (4)
From equations (3) and (4),
We can conclude that \[\angle A,\angle DCB\] and \[\angle ADC,\angle B\] are pairs of supplementary angles and from the concept we have discussed earlier we can conclude that \[\square ABCD\] is a cyclic quadrilateral.
Hence Proved.
Note:
1) The concept given by “opposite angles of a cyclic quadrilateral are always Supplementary” is very much essential to prove any quadrilateral as a cyclic quadrilateral.
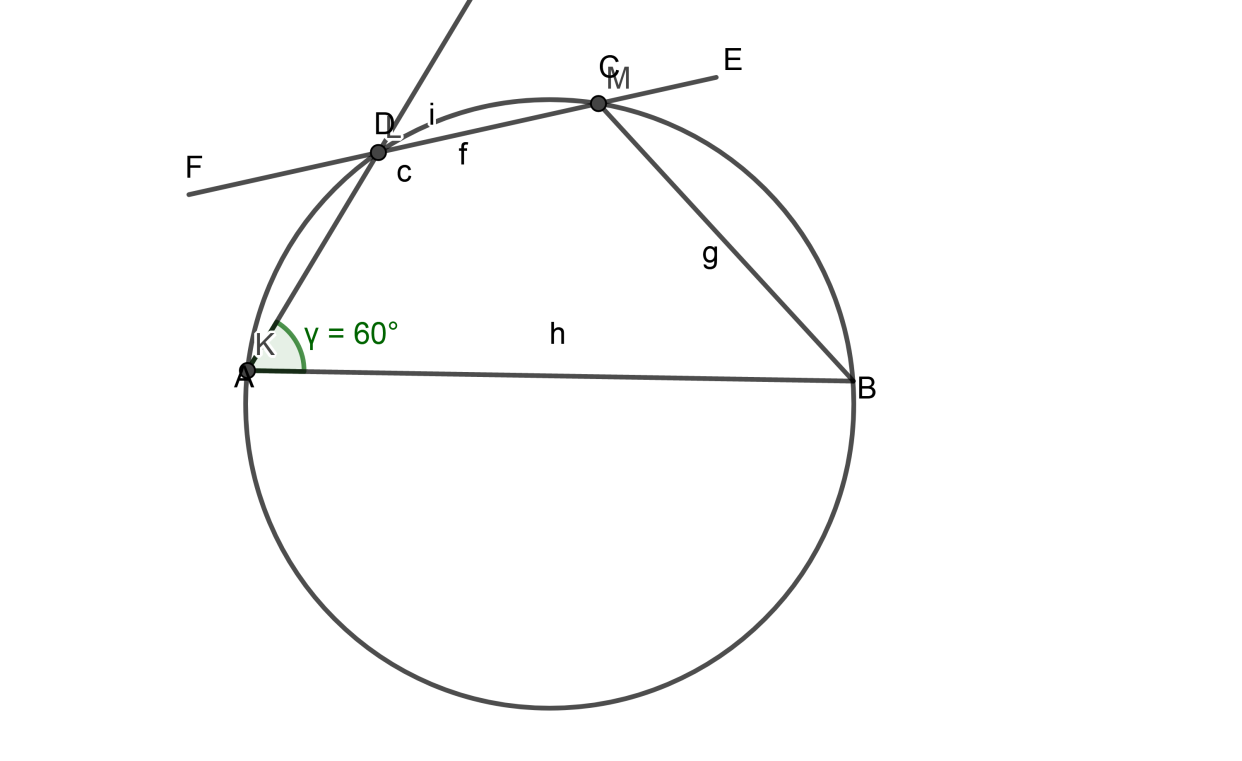
2) I have inscribed above the quadrilateral in a circle geometrically therefore it is proved experimentally also. I have taken the mentioned angle as \[60{}^\circ \].