Question

ABCD is a parallelogram (see figure below). The ratio of DE to EC is 1:3. Height AE has a length of 3. If quadrilateral ABCE has an area of 21, what is the area of ABCD?

Answer 1

Hint:
First, break quadrilateral ABCE into two pieces: A \[3 \times 3x\] rectangle and a right triangle with a base of $x$ and a height of 3.

Formula used:
We know that,
Area of rectangle is \[\left( {base} \right)\; \times \;\left( {height} \right)\]
Area of right angle triangle is \[\dfrac{1}{2} \times base \times height\]

Complete step by step answer:

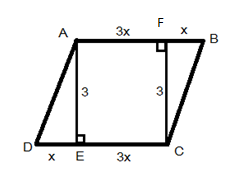
It is given that the ratio of DE to EC is 1:3
Let us consider \[DE{\rm{ }} = {\rm{ }}x\] and\[EC{\rm{ }} = 3x\],
Also given that area of quadrilateral ABCE 21unit.
Therefore, the area of quadrilateral ABCE is given by the following equation:
We can see the picture, we can come to a conclusion that,
 Area of quadrilateral ABCE is combination of Area of rectangle and right angle triangle\[BCF\]
The area of quadrilateral ABCE =area of the rectangle + area of the triangle.
The area of quadrilateral ABCE = \[\left( {3 \times 3x} \right) + \dfrac{1}{2} \times 3x\]
Solve and we get,
\[ = 9x + 1.5x\]
The area of the quadrilateral \[ = 10.5x\]
Now, it is given that ABCE has an area of 21,
Hence by equating the area we get,
\[\Rightarrow 21 = 10.5x\]
Hence by solving the above equation, we get
\[\Rightarrow x = 2\]
Now, we have to find the area of Quadrilateral ABCD.
We know that the Quadrilateral ABCD is a parallelogram,
So we can use the formula of parallelogram,
Here base of the parallelogram is found by adding $DE \text{ and } EC$
$\Rightarrow DE+EC=x+3x=4x$
We know that height is given as 3,
Area of the parallelogram \[ = {\rm{ }}\left( {base} \right)\; \times \;\left( {height} \right)\]
Let us substitute base, height and \[x = 2\] in the area formula, we get
\[\Rightarrow Area = 4\left( 2 \right) \times 3\]
\[\Rightarrow Area = 24{\rm{ }}uni{t^2}\]

$\therefore$ The area of Quadrilateral ABCD is \[24{\rm{ }}uni{t^2}\]

Note:
A parallelogram is a special type of quadrilateral that has equal and parallel opposite sides. The opposite sides of a parallelogram are equal in length. Diagonals of a parallelogram bisect each other.