Question

ABCD is a parallelogram. Points P and Q are taken on the sides AB and AD respectively and the perpendicular PRQA is formed. If $\angle C={{40}^{\circ }}$ find $\angle R\text{ and }\angle P$

Answer 1

Hint: For solving and better understanding of the question, we will first draw a diagram. As per question, a parallelogram PRQA is formed using two points P and Q on sides AB and AD respectively. We will prove that corresponding sides of both parallelograms are parallel which will imply that corresponding angles are also equal which will give us one of the required angles. After that, we will use the property of parallelogram that, sum of adjacent angles is equal to ${{180}^{\circ }}$ to find the other required angle.

Complete step-by-step answer:
Let us first draw diagram for better understanding of question:

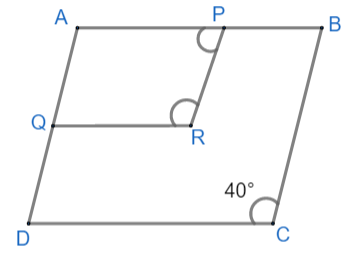
Here, we are given parallelogram ABCD. P and Q are two points on AB and AD respectively. PRQA forms a parallelogram. We are given that $\angle BCD={{40}^{\circ }}$ and we have to find $\angle PRQ\left( \angle R \right)\text{ and }\angle \text{APR}\left( \angle P \right)$
As we know, opposite sides of parallelograms are parallel. Therefore, for parallelogram ABCD,
\[AD\parallel BC\cdots \cdots \cdots \cdots \left( 1 \right)\]
And for parallelogram AQRP,
\[AQ\parallel PR\]
Since AD is just an extended line of AQ therefore both lines are parallel to the same line.
Hence, we can say that $AD\parallel PR$
Now from (1) we can say that $BC\parallel PR$
Also for parallelogram ABCD,
\[AD\parallel DC\cdots \cdots \cdots \cdots \left( 2 \right)\]
And for parallelogram APRQ,
\[AP\parallel QR\]
Since AB is just an extended line of AP, therefore both lines are parallel to the same line.
Hence, we can say that $AB\parallel QR$
Now from (1) we can say that $DC\parallel QR$
As we concluded that $BC\parallel PR$ and $DC\parallel QR$ therefore, they will form same angle that is $\angle BCD=\angle PRQ$
We are given value of $\angle BCD$ which is ${{40}^{\circ }}$ therefore, $\angle R={{40}^{\circ }}$
As PRQA is a parallelogram, therefore, sum of any two adjacent angles will be equal to ${{180}^{\circ }}$
Let us take $\angle R\text{ and }\angle P$ both these angles are adjacent. Therefore,
\[\angle R+\angle P={{180}^{\circ }}\]
As we know $\angle R={{40}^{\circ }}$ therefore,
\[\begin{align}
  & {{40}^{\circ }}+\angle P={{180}^{\circ }} \\
 & \Rightarrow \angle P={{140}^{\circ }} \\
\end{align}\]
Hence, we have found that $\angle R={{40}^{\circ }}\text{ and }\angle P={{140}^{\circ }}$

Note: Students should note that, both pairs of corresponding sides should be parallel for the angle to be equal. Also, if students cannot remember property of parallelogram that sum of adjacent angles is equal to ${{180}^{\circ }}$ then they can consider it as parallel lines with transversal and hence, sum of interior angles is equal to ${{180}^{\circ }}$