Question

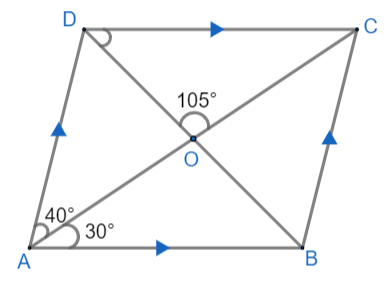
ABCD is a parallelogram in which \[\angle DAC={{40}^{\circ }},\angle BAC={{30}^{\circ }},\angle DOC={{105}^{\circ }}\] then $\angle CDO$ equals
\[\begin{align}
  & A{{.75}^{\circ }} \\
 & B{{.70}^{\circ }} \\
 & C{{.40}^{\circ }} \\
 & D{{.45}^{\circ }} \\
\end{align}\]

Answer 1

Hint: Here, we are given three angles and we have to find the value of $\angle CDO$. For this, we will use various properties of lines and angles and also the sum of angles of a triangle property. Properties which we will use are
(i) When two lines intersect each other, vertically opposite angles are equal.
(ii) When two lines are parallel and a transversal intersects them, then alternate interior angles formed are equal.
(iii) Sum of angles of a triangle is equal to ${{180}^{\circ }}$

Complete step by step answer:
In the given triangle, we are given \[\angle DAC={{40}^{\circ }},\angle BAC={{30}^{\circ }},\angle DOC={{105}^{\circ }}\] and we have to find $\angle CDO$.
As we know, AC and BD are diagonals of parallelograms. Hence, intersect each other.
Hence, $\angle AOB\text{ and }\angle COD$ are vertically opposite angles and thus they are equal.
We find that $\angle AOB=\angle COD={{105}^{\circ }}$. Therefore, $\angle AOB={{105}^{\circ }}$
As we can see OAB forms a triangle, we can use sum of angles property which states that sum of angles of a triangle is ${{180}^{\circ }}$.
As calculated earlier $\angle AOB={{105}^{\circ }}$
We are given $\angle OAB={{30}^{\circ }}$. Putting them in above equation, we get:
\[\begin{align}
  & {{105}^{\circ }}+{{30}^{\circ }}+\angle OBA={{180}^{\circ }} \\
 & \Rightarrow \angle OBA={{180}^{\circ }}-{{135}^{\circ }} \\
 & \Rightarrow \angle OBA={{45}^{\circ }}=\angle ABD \\
\end{align}\]
Now, as we know opposite sides of a parallelogram are always parallel, therefore, AB and CD are parallel and BD being diagonal acts as transversal. Therefore, alternate interior angles are equal. Hence, \[\angle ABD=\angle BDC={{45}^{\circ }}\]
Therefore, option D is the correct answer.

Note: Students should remember all the properties of lines and angles. These types of questions can be solved by many methods. We can also solve it first by finding angle OCD which is equal to angle CAB being alternate interior angle and then using the sum of angles of a triangle property in triangle OCD to find the required angle CDO.