Question

ABCD is a parallelogram. If L and M are midpoints on BC and CD respectively, then write AL and AM in terms of AB and AD.

Answer 1

Hint: Join the points A and C. Use vector law of addition for triangles $\Delta ACL$ and $\Delta AMC$. Use the fact that L and M are midpoints of side BC and CD respectively. Also, use that opposite sides of a parallelogram are equal to simplify the equations.

Complete step-by-step answer:
We have a parallelogram ABCD, with L and M as midpoints of BC and CD. We have to write AL and AM in terms of AB and AD.
We will join the points A and C, as shown in the figure.

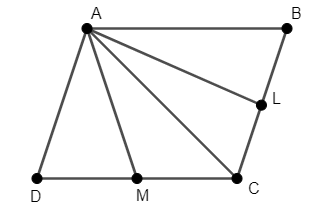
We know that in a triangle, the vector law of addition says that the sum of two vectors is equal to the third vector.
Thus, in $\Delta ALC$, we have $\overset{\to }{\mathop{AL}}\,+\overset{\to }{\mathop{LC}}\,=\overset{\to }{\mathop{AC}}\,.....\left( 1 \right)$.
As L is the midpoint of BC, we have $\overset{\to }{\mathop{LC}}\,=\dfrac{1}{2}\overset{\to }{\mathop{BC}}\,.....\left( 2 \right)$.
Substituting equation (2) in equation (1), we have $\overset{\to }{\mathop{AL}}\,+\dfrac{1}{2}\overset{\to }{\mathop{BC}}\,=\overset{\to }{\mathop{AC}}\,$.
Rearranging the terms of the above equation, we have $\overset{\to }{\mathop{AL}}\,=\overset{\to }{\mathop{AC}}\,-\dfrac{1}{2}\overset{\to }{\mathop{BC}}\,.....\left( 3 \right)$.
Similarly, in $\Delta AMC$, we have $\overset{\to }{\mathop{AM}}\,+\overset{\to }{\mathop{MC}}\,=\overset{\to }{\mathop{AC}}\,.....\left( 4 \right)$.
As M is the midpoint of CD, we have $\overset{\to }{\mathop{MC}}\,=\dfrac{1}{2}\overset{\to }{\mathop{CD}}\,.....\left( 5 \right)$.
Substituting equation (5) in equation (4), we have $\overset{\to }{\mathop{AM}}\,+\dfrac{1}{2}\overset{\to }{\mathop{CD}}\,=\overset{\to }{\mathop{AC}}\,$.
Rearranging the terms of the above equation, we have $\overset{\to }{\mathop{AM}}\,=\overset{\to }{\mathop{AC}}\,-\dfrac{1}{2}\overset{\to }{\mathop{CD}}\,.....\left( 6 \right)$.
Adding equation (3) and (6), we have $\overset{\to }{\mathop{AL}}\,+\overset{\to }{\mathop{AM}}\,=\overset{\to }{\mathop{AC}}\,-\dfrac{1}{2}\overset{\to }{\mathop{BC}}\,+\overset{\to }{\mathop{AC}}\,-\dfrac{1}{2}\overset{\to }{\mathop{CD}}\,$.
Simplifying the above equation, we have $\overset{\to }{\mathop{AL}}\,+\overset{\to }{\mathop{AM}}\,=\overset{\to }{\mathop{2AC}}\,-\dfrac{1}{2}\left( \overset{\to }{\mathop{BC}}\,+\overset{\to }{\mathop{CD}}\, \right).....\left( 7 \right)$.
As ABCD is a parallelogram, its opposite sides are equal. Thus, we have $\overset{\to }{\mathop{BC}}\,=\overset{\to }{\mathop{AD}}\,,\overset{\to }{\mathop{CD}}\,=\overset{\to }{\mathop{AB}}\,.....\left( 8 \right)$.
Substituting equation (8) in equation (7), we have $\overset{\to }{\mathop{AL}}\,+\overset{\to }{\mathop{AM}}\,=\overset{\to }{\mathop{2AC}}\,-\dfrac{1}{2}\left( \overset{\to }{\mathop{AD}}\,+\overset{\to }{\mathop{AB}}\, \right).....\left( 9 \right)$.
In $\Delta ABC$, we have $\overset{\to }{\mathop{AB}}\,+\overset{\to }{\mathop{BC}}\,=\overset{\to }{\mathop{AC}}\,.....\left( 10 \right)$.
Substituting equation (10) in equation (9), we have $\overset{\to }{\mathop{AL}}\,+\overset{\to }{\mathop{AM}}\,=2\left( \overset{\to }{\mathop{AB}}\,+\overset{\to }{\mathop{BC}}\, \right)-\dfrac{1}{2}\left( \overset{\to }{\mathop{AD}}\,+\overset{\to }{\mathop{AB}}\, \right)$.
Simplifying the above equation, we have $\overset{\to }{\mathop{AL}}\,+\overset{\to }{\mathop{AM}}\,=2\left( \overset{\to }{\mathop{AB}}\,+\overset{\to }{\mathop{AD}}\, \right)-\dfrac{1}{2}\left( \overset{\to }{\mathop{AD}}\,+\overset{\to }{\mathop{AB}}\, \right)=\dfrac{3}{2}\left( \overset{\to }{\mathop{AB}}\,+\overset{\to }{\mathop{AD}}\, \right)$.
Hence, for the given parallelogram ABCD, we have $\overset{\to }{\mathop{AL}}\,+\overset{\to }{\mathop{AM}}\,=\dfrac{3}{2}\left( \overset{\to }{\mathop{AB}}\,+\overset{\to }{\mathop{AD}}\, \right)$.

Note: It’s necessary to use the vector law of addition for triangles to solve this question. Otherwise, we won’t be able to solve the question. One must also remember the fact that the opposite sides of a parallelogram are equal.