Question

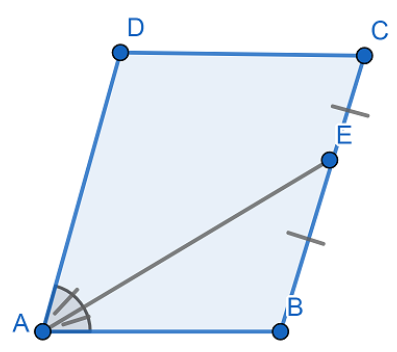
ABCD is a parallelogram. If $E$ is mid-point of $BC$ and $AE$ is the bisector of $\angle A$, prove that $AB=\dfrac{1}{2}AD$.

Answer 1

Hint: First we list all the information given in the question and understand the diagram given. Then, we use the property of a parallelogram. As given in the question $E$ is the mid-point of $BC$ and $AE$ is the bisector of $\angle A$, we form two equations using this and compare both equations. Then by using the mid-point theorem we reach our desired result.

Complete step-by-step solution:
We have given that $ABCD$ is a parallelogram. $E$ is the mid-point of $BC$ and $AE$ is the bisector of $\angle A$.
We have to prove that $AB=\dfrac{1}{2}AD$
We know that the opposite sides of a parallelogram are parallel and equal to each other.
So, we have $AB\parallel CD$ and $AD\parallel BC$.
We have given that $AE$ is the bisector of $\angle A$. We know that angle bisector bisects angle into two equal parts.
So, we have $\angle BAE=\angle DAE...........(i)$
Also, we have given that $E$ is the mid-point of $BC$.
So, $BE=CE$
As we know that alternate angles in the same segment are equal to each other.
If $AD\parallel BC$ then, we have $\angle BEA=\angle DAE............(ii)$
When we compare equation (i) and equation (ii), we get
$\angle BAE=\angle BEA$
We know that the opposite sides of equal angles are also equal.
So, $AB=BE.........(iii)$
Now, we have given that $E$ is the mid-point of $BC$.
So, $BE=\dfrac{1}{2}BC...........(iv)$ As $BE=CE$
When we put the value of $BE$ from equation (iii), we get
$AB=\dfrac{1}{2}BC$
Also, we know that $AD=BC$ [opposite sides of a parallelogram are parallel and equal to each other.]
So, $AB=\dfrac{1}{2}AD$
Hence proved

Note: Students must have a good understanding of the figures to solve this type of question. Also, students must have knowledge about the properties of parallelograms, alternate angles, and parallel lines. Also, we have used the mid-point property and angle bisector property to solve this question.