
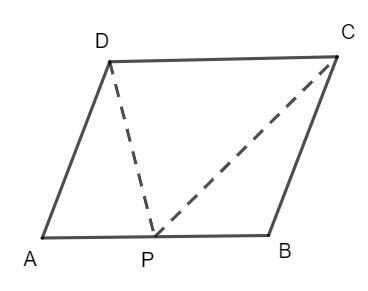
ABCD is a parallelogram as shown in the figure. If AB = 2AD and P is midpoint of AB, then what is the value of \[\angle CPD\] ?
(a). 90°
(b). 60°
(c). 45°
(d). 135°

Answer
624.6k+ views
Hint: Use the property of the parallelogram that the adjacent angles are supplementary. Then find the angle CPD in terms of the adjacent angles and find its value.
Complete step-by-step answer:
ABCD is a parallelogram, hence, the adjacent angles of the parallelogram are supplementary, that is, the sum of angles is 180°.
\[\angle A + \angle B = 180^\circ ............(1)\]
It is given that AB = 2 AD, then we have:
\[AD = \dfrac{{AB}}{2}..............(2)\]
It is given that P is the midpoint of AB. Then, we have the following:
\[AP = \dfrac{{AB}}{2}..........(3)\]
From equation (2) and equation (3), we have:
\[AD = AP\]
Hence, the triangle APD is an isosceles triangle.
The sum of the angles of the triangle APD is 180°.
\[\angle APD + \angle ADP + \angle A = 180^\circ \]
\[2\angle APD + \angle A = 180^\circ \]
Solve for the angle APD to get as follows:
\[\angle APD = 90^\circ - \dfrac{{\angle A}}{2}............(4)\]
The opposite sides of the parallelogram are equal. Hence, AD = BC, then we have:
\[BP = BC\]
Then, the triangle BPC is also an isosceles triangle.
The sum of the angles of the triangle BPC is 180°.
\[\angle BPC + \angle BCP + \angle B = 180^\circ \]
\[2\angle BPC + \angle B = 180^\circ \]
Solve for the angle BPC to get as follows:
\[\angle BPC = 90^\circ - \dfrac{{\angle B}}{2}............(5)\]
The angle on a straight line add up to 180°, then we have on line APB as follows:
\[\angle BPC + \angle CPD + \angle APD = 180^\circ \]
Using equations (4) and (5), we get:
\[90^\circ - \dfrac{{\angle B}}{2} + \angle CPD + 90^\circ - \dfrac{{\angle A}}{2} = 180^\circ \]
Simplifying, we have:
\[180^\circ - \dfrac{{\angle B + \angle A}}{2} + \angle CPD = 180^\circ \]
Canceling 180° on both sides, we have:
\[\angle CPD = \dfrac{{\angle B + \angle A}}{2}\]
From equation (1), we have:
\[\angle CPD = \dfrac{{180^\circ }}{2}\]
\[\angle CPD = 90^\circ \]
Hence, the correct answer is option (a).
Note: You can also find the angles CDP and DCP in terms of the angle D and angle C respectively and then find the angle CPD using the properties of the triangle.
Complete step-by-step answer:

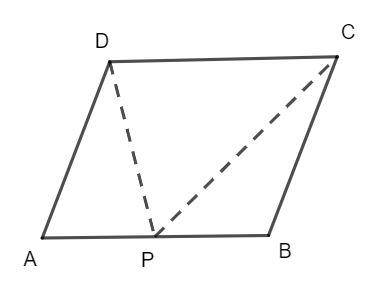
ABCD is a parallelogram, hence, the adjacent angles of the parallelogram are supplementary, that is, the sum of angles is 180°.
\[\angle A + \angle B = 180^\circ ............(1)\]
It is given that AB = 2 AD, then we have:
\[AD = \dfrac{{AB}}{2}..............(2)\]
It is given that P is the midpoint of AB. Then, we have the following:
\[AP = \dfrac{{AB}}{2}..........(3)\]
From equation (2) and equation (3), we have:
\[AD = AP\]
Hence, the triangle APD is an isosceles triangle.
The sum of the angles of the triangle APD is 180°.
\[\angle APD + \angle ADP + \angle A = 180^\circ \]
\[2\angle APD + \angle A = 180^\circ \]
Solve for the angle APD to get as follows:
\[\angle APD = 90^\circ - \dfrac{{\angle A}}{2}............(4)\]
The opposite sides of the parallelogram are equal. Hence, AD = BC, then we have:
\[BP = BC\]
Then, the triangle BPC is also an isosceles triangle.
The sum of the angles of the triangle BPC is 180°.
\[\angle BPC + \angle BCP + \angle B = 180^\circ \]
\[2\angle BPC + \angle B = 180^\circ \]
Solve for the angle BPC to get as follows:
\[\angle BPC = 90^\circ - \dfrac{{\angle B}}{2}............(5)\]
The angle on a straight line add up to 180°, then we have on line APB as follows:
\[\angle BPC + \angle CPD + \angle APD = 180^\circ \]
Using equations (4) and (5), we get:
\[90^\circ - \dfrac{{\angle B}}{2} + \angle CPD + 90^\circ - \dfrac{{\angle A}}{2} = 180^\circ \]
Simplifying, we have:
\[180^\circ - \dfrac{{\angle B + \angle A}}{2} + \angle CPD = 180^\circ \]
Canceling 180° on both sides, we have:
\[\angle CPD = \dfrac{{\angle B + \angle A}}{2}\]
From equation (1), we have:
\[\angle CPD = \dfrac{{180^\circ }}{2}\]
\[\angle CPD = 90^\circ \]
Hence, the correct answer is option (a).
Note: You can also find the angles CDP and DCP in terms of the angle D and angle C respectively and then find the angle CPD using the properties of the triangle.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
Who is known as the "Little Master" in Indian cricket history?

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Who Won 36 Oscar Awards? Record Holder Revealed

Why is there a time difference of about 5 hours between class 10 social science CBSE

Explain the Treaty of Vienna of 1815 class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE




