Question

ABCD is a parallelogram as shown in fig. If AB=2AD and P is mid-point of AB, then $\angle CPD$ is equal to:
$\left( a \right){90^\circ}$
$\left( b \right){60^\circ}$
$\left( c \right){45^\circ}$
$\left( d \right){135^\circ}$

Answer 1

Hint – In this problem use the concept that opposite sides of a parallelogram are equal so AD=BC and that angles opposite to equal sides are equal thus $\angle APD$ = $\angle ADP$ and $\angle BPC$ = $\angle PCB$. These concepts along with the fact that adjacent angles of parallelogram make ${180^\circ}$ will help getting the required angle.

Complete step-by-step answer:

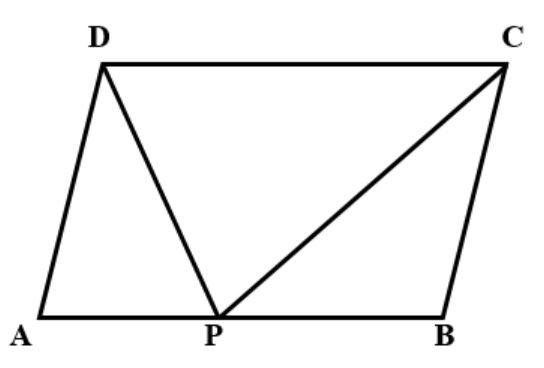
Since P is the midpoint of AB. From this we conclude that
AP = PB=$\dfrac{1}{2}$AB
$\because $AB= 2AD, so from this we get
AP=PB=$\dfrac{1}{2}$AD$ \times $2= AD ………… (i)
Also as we know that in case of parallelogram opposite sides are equal and parallel therefore,
AD = BC
So, from equation (1) $\Delta $APD and $\Delta $BPC are isosceles as AP = AD and PB = BC and with PD and PC as bases respectively
Also, $\angle $APD = $\angle $ADP and $\angle $BPC = $\angle $PCB (as angles opposite to equal sides are also equal)……….. (ii)
Now, $\angle $APD = $\angle $PDC and $\angle $BPC = $\angle $PCD (Alternate Angles between the parallels AB and CD)………… (iii)
So from equations (ii) and (iii)
$\angle $ADP = $\angle $ PDC
$ \Rightarrow $$\angle $ ADP + $\angle $PDC = $\angle $ ADC = 2$\angle $PDC…… (iv)
And $\angle $ PCB = $\angle $PCD
$ \Rightarrow $ $\angle $PCD + $\angle $PCB =$\angle $BCD = 2$\angle $PCD…….. (v)
Now add equations (iv) and (v) we get
$\angle $ADC +$\angle $BCD = 2($\angle $PDC +$\angle $PCD)……. (vi)
From the property of parallelogram that sum of adjacent angles of parallelogram is 180°.
So from equation (vi)
2($\angle $PDC+$\angle $PCD) =180°
$\therefore $ $\angle $PDC + $\angle $PCD = 90°…………………… (A)
Now in $\Delta $PDC,
By angle sum property of triangle the sum of all interior angles is equal to 180°
$\angle $CPD = 180° - ($\angle $PDC + $\angle $PCD)
$\therefore $$\angle $CPD = 180° - 90° = 90° (from equation A)
So this is the required answer.
Hence option (a) is correct.

Note – A parallelogram is a quadrilateral with opposite sides parallel and equal. A quadrilateral with equal sides is called a rhombus and a parallelogram whose all angles are right angles is called a rectangle. It is advised to have a good understanding of the figures involved in geometry while solving problems of this kind as it helps in figuring out the alternate angels and other angel properties.