Question

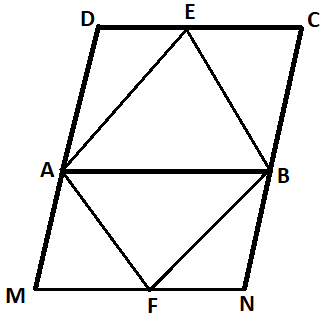
ABCD is a parallelogram. AE and AF are bisectors of interior and exterior angles respectively at A and BE and BF are bisectors of interior and exterior angles respectively at B. Show that AFBE is a parallelogram.

Answer 1

Hint: Here given a parallelogram ABCD, and we are asked to prove that AFBE is also a parallelogram. The properties of a parallelogram are the opposite sides and angles are equal, the adjacent angles are supplementary and the most important property is that the diagonals bisect each other. The property of supplementary angles and the linear pair angles is also used here.

Complete step-by-step answer:
Given that ABCD is a parallelogram.
AE and BE bisects the angle $ \angle BAD $ and $ \angle CBA $ respectively.
AF and BF bisects the $ \angle BAM $ and $ \angle ABN $ respectively.
We have to show that AFBE is a parallelogram.
Given that AE bisects the angle $ \angle BAD $ ,
 $ \Rightarrow \angle DAE = \angle EAB $
 $ \therefore \angle DAB = \angle DAE + \angle EAB $
BE bisects the angle $ \angle CBA $ ,
 $ \Rightarrow \angle CBE = \angle EBA $
 $ \therefore \angle CBA = \angle CBE + \angle EBA $
Given that ABCD is a parallelogram,
So the adjacent angles in a parallelogram are supplementary.
 $ \therefore \angle DAB + \angle CBA = {180^ \circ } $
Substituting the expression of the angles $ \angle DAB $ and $ \angle CBA $ , as given below:
 $ \Rightarrow \angle DAB + \angle CBA = {180^ \circ } $
 $ \Rightarrow \left( {\angle DAE + \angle EAB} \right) + \left( {\angle CBE + \angle EBA} \right) = {180^ \circ } $
We know that $ \angle DAE = \angle EAB $ and $ \angle CBE = \angle EBA $ , substituting these expressions in the above equation:
 $ \Rightarrow 2\angle EAB + 2\angle EBA = {180^ \circ } $
 $ \Rightarrow 2\left( {\angle EAB + \angle EBA} \right) = {180^ \circ } $
 $ \Rightarrow \angle EAB + \angle EBA = {90^ \circ } $
Now consider the triangle $ \Delta EAB $ , in that the sum of the angles $ \angle EAB $ and $ \angle EBA $ is $ {90^ \circ } $ .
The sum of the angles in the triangle is $ {180^ \circ } $ ,
 $ \Rightarrow \angle EAB + \angle AEB + \angle EBA = {180^ \circ } $
 $ \Rightarrow {90^ \circ } + \angle AEB = {180^ \circ } $
 $ \therefore \angle AEB = {90^ \circ } $
By doing the same process we can also obtain that $ \angle AFB = {90^ \circ } $ .
 $ \therefore \angle AEB = {90^ \circ } $
Given that AF bisects $ \angle BAM $ ,
 $ \Rightarrow \angle BAF = \angle FAM $
 $ \Rightarrow \angle BAM = \angle BAF + \angle FAM $
Consider the angle $ \angle A $ , it is a linear pair , with the sum of two angles, as given below:
 $ \Rightarrow \angle DAB + \angle BAM = {180^ \circ } $
 \[ \Rightarrow \left( {\angle DAE + \angle EAB} \right) + \left( {\angle BAF + \angle FAM} \right) = {180^ \circ }\]
 \[ \Rightarrow 2\angle EAB + 2\angle BAF = {180^ \circ }\]
 \[ \Rightarrow 2\left( {\angle EAB + \angle BAF} \right) = {180^ \circ }\]
 \[ \Rightarrow \angle EAB + \angle BAF = {90^ \circ }\]
We know that \[\angle EAB + \angle BAF = \angle EAF\] ,
 \[\therefore \angle EAF = {90^ \circ }\]
Hence till now be obtained in the quadrilateral AFBE that,
 $ \Rightarrow \angle AEB = {90^ \circ },\angle AEB = {90^ \circ } $ and \[\angle EAF = {90^ \circ }\] .
The sum of the angles in a quadrilateral is $ {360^ \circ } $ , hence the other angle $ \angle EBF = {90^ \circ } $ .
Here the opposite angles in the quadrilateral AFBE are equal, hence AFBE is a parallelogram.

Hence proved.

Note:
 Please note that there is a difference between linear pair of angles and supplementary angles. Linear pairs of angles are the two angles which are adjacent and share a common vertex, a linear pair forms a straight line which makes an angle of $ {180^ \circ } $ . But the supplementary angles need not be adjacent angles, any two angles which add up to give $ {180^ \circ } $ are called supplementary angles.