Question

ABCD is a parallelogram, AD is produced to E so that DE = DC and ED produced meets AB produced in F. Prove that BF = BC.

Answer 1

Hint: At first, we need to draw the diagram. Consider a triangle DCE and then prove that angle DCE and DEC are equal. After that consider the triangle AEF and from that use the property of parallelogram to prove the required answer.

Complete step-by-step answer:
In the question, it is given that ABCD is a parallelogram, AD is produced or extended to E such that DE = DC and then EC is joined. Now both EC and AB are extended to join at point F. We have to prove that BF and FC are equal. First, we take note of what is given to us. ABCD is a parallelogram and DE = DC.

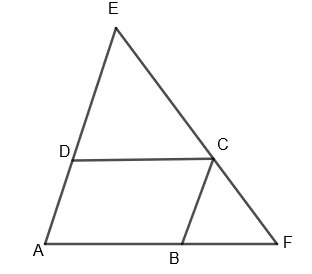
So, let’s consider the triangle DCE.
DC = DE [given]
We know that angles opposite to equal sides are equal, so
\[\angle DCE=\angle DEC\]
Now, as we know that ABCD is a parallelogram, so \[AB||CD\] as opposite sides are parallel to each other. We can say that \[\angle DCE=\angle BFC\] as DC is parallel to AD. So, the corresponding angles should be equal. So, we can write, \[\angle DCE=\angle BFC\] as we know that \[\angle DCE=\angle DEC\].
Now, let us consider the triangle AEF, we can see that
\[\angle AEF=\angle AFE\]
As angles of the triangle are equal then their opposite sides are equal. So, AF = AE.
Now, from the figure, we can say that, AF = AB + BF and AE = AD + DE.
So, AB + BF = AD + DE
As ABCD is a parallelogram, AB = CD because of the property that opposite sides are equal. Now from the figure we can say that,
AF = AB + BF
And, AE = AD + DE
So, AB + BF = AD + DE
From the figure, we can also say that, AB = DE.
As we have written,
AB + BF = AD + DE
We can also write,
BF = AD
Now once again we will use the property of the parallelogram where opposite sides are equal. So, we can say AD = BC.
Hence BF = BC
Hence proved.

Note: Students should know the properties of a parallelogram. They should also know about the properties of the triangle and parallel lines to solve these kinds of problems.