Question

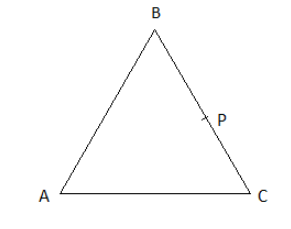
ABC is a triangle and P is any point on BC. If \[\overline {PQ} \] is the resultant of the vectors \[\overline {AP} ,\overline {PB} \] and \[\overline {PC} \]then ACQB is

Answer 1

Hint:

A vector has magnitude and direction.

the vector p=\[\overline {PQ} \]
The resultant vector is the vector sum of two or more vectors. It is the result of adding two or more vectors together. If displacement vectors A, B, and C are added together, the result will be vector R.
R=A+B+C.
Here it is given that \[\overline {PQ} \] is the resultant of the vectors \[\overline {AP} ,\overline {PB} \] and \[\overline {PC} \] using this we will find the value of\[\overline {CQ} \] and then relate it with\[\overline {AB} \]which helps in giving information about the required ACQB.

Complete step-by-step answer:
It is given that ABC is a triangle and P is any point on BC.
Also given that, \[\overline {PQ} \] is the resultant of the vectors \[\overline {AP} ,\overline {PB} \] and\[\overline {PC} \].
As we know that we can all the vectors to find the resultant we get,
 \[\overline {PQ} = \overline {AP} + \overline {PB} + \overline {PC} \]
Let us take \[\overline {PC} \]to the left hand side,
\[\overline {PQ} - \overline {PC} = \overline {AP} + \overline {PB} \]…(1)
If the direction of the vector \[\overline {PC} \]is changed then we have,\[\overline {PC} = - \overline {CP} \]
Let us substitute the \[\overline {PC} \] in equation (1) we get,
\[\overline {PQ} + \overline {CP} = \overline {AP} + \overline {PB} \]…(2)
Here we have added the vectors hence it will lead to the following resultant vectors,
\[\overline {CQ} = \overline {AB} \]
In the above equation the resultant vector of \[\overline {PQ} \]and \[\overline {CP} \] is\[\overline {CQ} \], the resultant vector of \[\overline {AP} \]and \[\overline {PB} \]is \[\overline {AB} \]
Now, we know if \[\overline {CQ} = \overline {AB} \]then
CQ= AB & CQ||AB which is nothing but the condition of a parallelogram.
So, ACQB is a parallelogram.

Note:

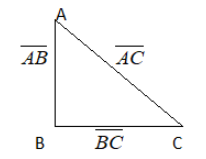
If ABC is a triangle
\[\overline {AB} \] & \[\overline {BC} \]are two vectors then the resultant vector is
\[\overline {AC} = \overline {AB} + \overline {BC} \]. We have used it in equation 2.
And the condition of a shape to be parallelogram is AB=CD and AB||CD.