Question

ABC is a triangle and AD is the median of the triangle. E is any point on the median ED. Which of the following options is correct?
[a] ar(ABE) = ar(ACE)
[b] BE = CE
[c] AB+BE = AC+CE
[d] $AE=\dfrac{CE+BE}{2}$

Answer 1

Hint: Solve the question option wise by checking which of the options is correct and which of the options is incorrect. For option [a] use the fact that the median of a triangle divides the triangle into two triangles of equal area. Hence prove that $ar\left( \Delta ADC \right)=ar\left( \Delta ABD \right)$ and $ar\left( \Delta EDC \right)=ar\left( \Delta EDB \right)$. Subtract the two equations and hence arrive at the result. For option [b] consider an example of a scalene triangle and E as point A and hence prove that BE may not be equal to CE. Similarly, prove the result for option [c]. Similarly, prove the result for option [d].

Complete step-by-step answer:
We will solve the question option wise.
Let us check options [b], [c] and [d] first.
Since E is any point in AD, let us consider the case when A coincides with E and $AC\ne AB$ as shown in the diagram below

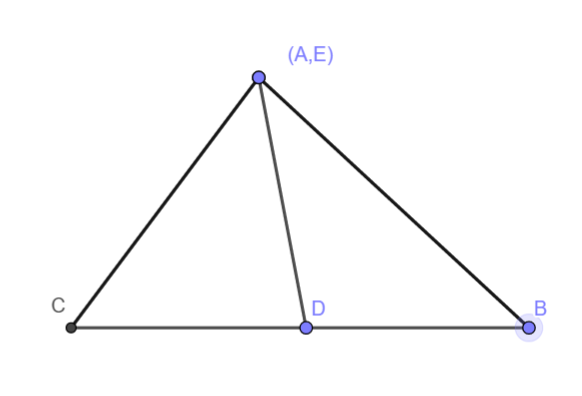
Now, we have $BE=AB$ and $CE=AC$
Since $AC\ne AB$, we have $BE\ne AE$
Hence option [b] is incorrect.
Also, we have$AB+BE=AB+AB=2AB$ and $AC+CE=AC+AC=2AC$
Since $AC\ne AB$, we have $AB+BE\ne AC+CE$
Hence option [c] is incorrect.
Also, we have $AE=0$
Since BE and CE are both positive, we have $\dfrac{BE+CE}{2}\ne 0$
Hence, we have $\dfrac{BE+CE}{2}\ne AE$
Hence option [b] is incorrect.
Now, let us consider a general triangle ABC, with AD as median and E a point on AD as shown below

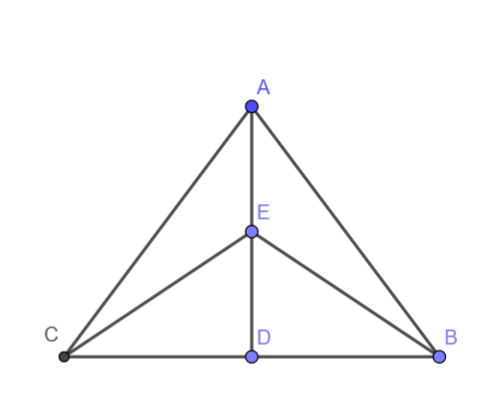
Claim: $ar\left( \Delta ACE \right)=ar\left( \Delta ABE \right)$
Proof:
We know the median of a triangle divides the triangle into two triangles of equal area. Since AD is the median of the triangle ABC, we have
$ar\left( \Delta ADC \right)=ar\left( \Delta ABD \right)\text{ }\left( i \right)$
Since ED is the median of the triangle EBC, we have
$ar\left( \Delta ECD \right)=ar\left( \Delta EBD \right)\text{ }\left( ii \right)$
Subtracting equation (ii) from equation (i), we get
$ar\left( \Delta ADC \right)-ar\left( \Delta ECD \right)=ar\left( \Delta ABD \right)-ar\left( \Delta EBD \right)$
From the figure, we have
$ar\left( \Delta ACD \right)-ar\left( \Delta ECD \right)=ar\left( \Delta ACE \right)$ and $ar\left( \Delta ABD \right)-ar\left( \Delta EBD \right)=ar\left( \Delta ABE \right)$
Hence, we have
$ar\left( \Delta AEC \right)=ar\left( \Delta ABE \right)$
Hence option [a] is correct.

Note: In mathematics in order to prove a result is correct, we need to give a formal proof and prove the result for all the possible conditions, and in order to prove that a result is incorrect, we need to come up with a case where the property fails to hold. This is known as proof by counterexample. In option [b], [c] and [d] we prove the results were incorrect by providing a counterexample.