Question

ABC is a right triangle, right angled at C. If p is the length of perpendicular from C to AB and a, b, c have usual meaning, then prove that:
(a) $pc=ab$
(b) $\dfrac{1}{{{p}^{2}}}=\dfrac{1}{{{a}^{2}}}+\dfrac{1}{{{b}^{2}}}$

Answer 1

Hint: At first draw the diagram according to the question. Then use the area of a right angle triangle formula, which is $\dfrac{1}{2}\times base\times height$, to prove the first part of the problem. Then by using Pythagoras theorem and the result from part (a) we will be able to prove part (b).

Complete step-by-step answer:
Let us first draw the diagram.

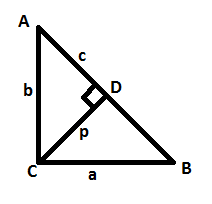
In the above diagram, ABC is a right triangle, right angled at C. CD is the perpendicular from C to AB.
It is given that length of CD is p, length of AB is c, length of BC is a, length of AC is b.
We know that the area formula of a right angle triangle is $\dfrac{1}{2}\times base\times height$.
Here we can find out the area of triangle ABC in two different ways.
If we take BC as our base, then AC will be the height. Therefore,
Area of triangle ABC $=\dfrac{1}{2}\times BC\times AC$.
We can put the lengths of BC and AC in the above expression. Therefore,
Area of triangle ABC $=\dfrac{1}{2}\times a\times b=\dfrac{ab}{2}........(1)$
Again we can take AB as our base the height will be CD. Therefore,
Area of triangle ABC $=\dfrac{1}{2}\times AB\times CD$.
We can put the lengths of AB and CD in the above expression. Therefore,
Area of triangle ABC $=\dfrac{1}{2}\times c\times p=\dfrac{pc}{2}......(2)$
Now both (1) and (2) are areas of triangle ABC. Therefore, they are equal.
$\dfrac{ab}{2}=\dfrac{pc}{2}$
We can cancel out the 2 from both the denominators. Therefore,
$\Rightarrow ab=pc......(3)$
Hence we proved that $pc=ab$.
Since, ABC is a right angle triangle we can apply Pythagoras theorem on ABC. That is,
$hypotenus{{e}^{2}}=bas{{e}^{2}}+heigh{{t}^{2}}$
In triangle ABC, hypotenuse is AB, base and height are BC and AC respectively. Therefore,
$A{{B}^{2}}=B{{C}^{2}}+A{{C}^{2}}$
Now we can put the lengths of AB, BC and AC in the above expression.
$\Rightarrow {{c}^{2}}={{a}^{2}}+{{b}^{2}}$
We will put the value of c from equation (3) in the above expression.
$\Rightarrow {{\left( \dfrac{ab}{p} \right)}^{2}}={{a}^{2}}+{{b}^{2}}$
$\Rightarrow \dfrac{{{a}^{2}}{{b}^{2}}}{{{p}^{2}}}={{a}^{2}}+{{b}^{2}}$
Now we will divide both sides of the equation by ${{a}^{2}}{{b}^{2}}$. Therefore,
$\Rightarrow \dfrac{{{a}^{2}}{{b}^{2}}}{{{p}^{2}}\times {{a}^{2}}{{b}^{2}}}=\dfrac{{{a}^{2}}+{{b}^{2}}}{{{a}^{2}}{{b}^{2}}}$
$\Rightarrow \dfrac{1}{{{p}^{2}}}=\dfrac{{{a}^{2}}}{{{a}^{2}}{{b}^{2}}}+\dfrac{{{b}^{2}}}{{{a}^{2}}{{b}^{2}}}$
$\Rightarrow \dfrac{1}{{{p}^{2}}}=\dfrac{1}{{{a}^{2}}}+\dfrac{1}{{{b}^{2}}}$
Hence, we proved that $\dfrac{1}{{{p}^{2}}}=\dfrac{1}{{{a}^{2}}}+\dfrac{1}{{{b}^{2}}}$.

Note: Alternatively, we can take AC as our base and BC as our height and by following the same steps we will get our result.