Question

ABC and BDE are two equilateral triangles such that “D” is the midpoint of BC. Ratio of the area of the triangles ABC and BDE is
A.$2:1$
B.$1:4$
C.$1:2$
D.$4:1$

Answer 1

Hint: We can draw the triangles. As D is the midpoint of BC, we can prove that the length of the smaller triangle is half of the bigger one. Then we can find the area of the 2 triangles. To get the required ratio, we can divide the area of the triangle and cancel the common terms.

Complete step-by-step answer:
We can draw diagrams with the given details for better understanding of the question.

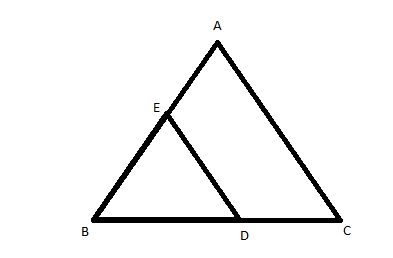
Let the length of the side of the triangle ABC, $BC = a$
It is given that D is the midpoint of BC.
So, BD will be half of BC.
$ \Rightarrow BD = \dfrac{{BC}}{2} = \dfrac{a}{2}$
We know that area of an equilateral triangle is given by the equation $A = \dfrac{{\sqrt 3 }}{4}{a^2}$
So, we can write the area of triangle ABC as ${A_1} = \dfrac{{\sqrt 3 }}{4}{a^2}$
Then the area of triangle BDE is ${A_2} = \dfrac{{\sqrt 3 }}{4}{\left( {\dfrac{a}{2}} \right)^2}$
$ \Rightarrow {A_2} = \dfrac{{\sqrt 3 }}{{4 \times 4}}{a^2}$
Now we need to find the ratio of area of triangle ABC to BDE.
It is given by,
$\dfrac{{{A_1}}}{{{A_2}}} = \dfrac{{\dfrac{{\sqrt 3 }}{4}{a^2}}}{{\dfrac{{\sqrt 3 }}{{4 \times 4}}{a^2}}}$
We can cancel the common terms. So, we get
$ \Rightarrow \dfrac{{{A_1}}}{{{A_2}}} = \dfrac{1}{{\dfrac{1}{4}}}$
We can multiply the numerator and denominator with 4.
 $ \Rightarrow \dfrac{{{A_1}}}{{{A_2}}} = \dfrac{4}{1}$
So, the required ratio is $4:1$.
Therefore, the correct answer is option D.

Note: Alternate method of solving this problem is given by,
We know that area of an equilateral triangle is proportional to the square of the side.
$ \Rightarrow A\,\alpha \,{a^2}$
Let ${A_1}$be the area of triangle ABC and ${A_2}$be the area of triangle BDE
Then by proportionality,
$ \Rightarrow \dfrac{{{A_1}}}{{{A_2}}} = \dfrac{{{a_1}^2}}{{{a_2}^2}}$ … (1)
It is given that D is the midpoint of BC.
So, BD will be half of BC.
$ \Rightarrow \dfrac{{{a_1}}}{{{a_2}}} = \dfrac{2}{1}$
Substituting this in equation (1), we get,
\[ \Rightarrow \dfrac{{{A_1}}}{{{A_2}}} = {\left( {\dfrac{2}{1}} \right)^2} = \dfrac{4}{1}\]
So, the required ratio is $4:1$.