Question

ABC and ADC are the two right triangles with common hypotenuse AC. Prove that \[\angle CAD = \angle CBD\].

Answer 1

Hint:- We had to only draw two triangles ABC and ADC such that they have a common hypotenuse AC and then we check whether the quadrilateral formed ABCD is a cyclic quadrilateral (i.e. sum of opposite angles is equal to 180 degrees).

Complete step-by-step answer:

As we know that AC is the hypotenuse of the triangles ABC and ADC then thee right angle triangles must be \[\angle B = 90^\circ \] and \[\angle D = 90^\circ \]

So, now let us draw triangles ABC and ADC such that they have common hypotenuse A

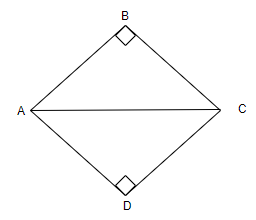
Now as we can see from the above figure that ABCD is a quadrilateral because it is a closed figure and has four sides.

Now according to the question.

\[\angle B = 90^\circ \] and \[\angle D = 90^\circ \]

So, \[\angle B + \angle D = 90^\circ + 90^\circ = 180^\circ \]

Now as we know that according to the property of cyclic quadrilateral which states that if the sum of opposite angles of a quadrilateral is equal to \[180^\circ \], then the quadrilateral must be a cyclic quadrilateral.

So, now we can draw a circle in which ABCD is a cyclic quadrilateral. So, we consider AC as a diameter and draw a circle because the line joining opposite vertices of a cyclic quadrilateral is the diameter of the circle in which the quadrilateral is inscribed. And join the points B and D.

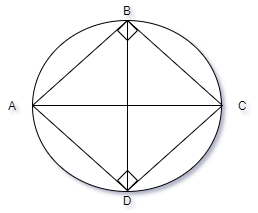
Now we can draw the segment CDABC in the above figure.

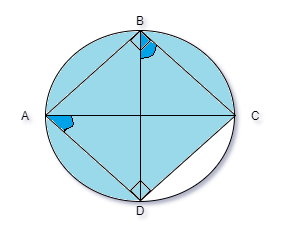
Now as we can see from the above figure that for the point C and D and the segment CDABC

\[\angle CAD\] and \[\angle CBD\] are the angles in the same segment.

So, as we know that the angles in the same segment of a circle are equal. So, \[\angle CAD = \angle CBD\]

Hence proved.

Note:- Whenever we come up with this type of problem then we first draw both of the triangles with common hypotenuse AC and then we had to check whether the quadrilateral formed ABCD is a cyclic quadrilateral i.e. sum of opposite angles of the quadrilateral ABCD is equal to \[180^\circ \]. And after that we draw a segment CDABC on the circle circumscribing the cyclic quadrilateral such that \[\angle CAD\] and \[\angle CBD\] are the angles in the same segment. And after that we can say that \[\angle CAD\] and \[\angle CBD\] are equal because angles on the same segment are equal.