Question

AB and CD are two parallel chords of length 8cm and 6cm respectively. If they are 1cm apart and lie on the same side of the centre of the circle. The radius of the circle is
A) 3 cm
B) 6 cm
C) 5 cm
D) 8 cm

Answer 1

Hint: The fixed point is called the centre of the circle and the distance from the centre to a point on the circle is called the radius of the circle. A chord of a circle is a straight line segment whose endpoints both lie on the circumference of the circle. Diameter is the biggest chord of the circle as it passes through the circle.
Perpendicular drawn from the centre to any chord of the circle bisects the chord into two equal parts.

Complete step-by-step answer:
Given:
AB = 8cm and CD = 6cm are two parallel chords of a circle with centre O.
The distance between AB and CD is 1cm.
To find out the radius of the given circle:

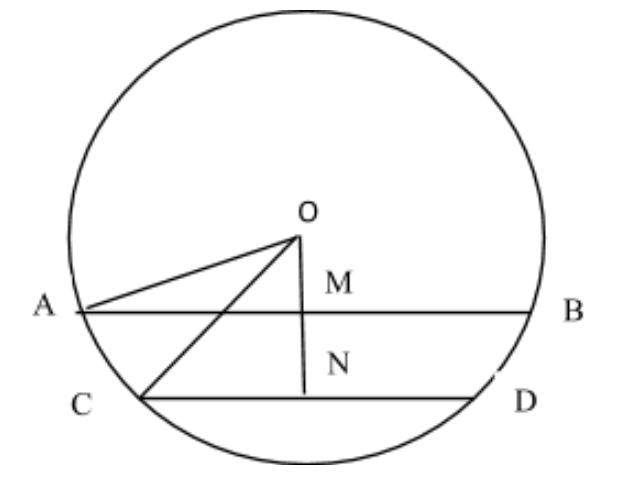
We drop a perpendicular OM on AB from O. OM meets AB at M.
OM is extended to meet CD at N.
OA and OC are joined.
∴ OA and OC are radius of the circle
As, $OM\mathrm{\perp }AB\Rightarrow \mathrm{\angle }AMO={90}^{\circ }=\mathrm{\angle }CNO$
(corresponding angles of two parallel lines)
So, $ON\mathrm{\perp }CD$
So, MN is the distance between AB and CD
And we know that MN = 1cm
Let OM = x cm, then ON = (x+1)cm
As, $OM\mathrm{\perp }AB$
Therefore, $AM={\displaystyle \frac{1}{2}}AB\Rightarrow {\displaystyle \frac{1}{2}}\times 8cm=4cm$
Since, the perpendicular from the centre of a circle to any of its chords always bisect them
Again, $OM\mathrm{\perp }AB$
∴∆OAM is a right triangle with OA as hypotenuse.
So, by Pythagoras theorem, we get
$OA=\sqrt{O{M}^2+A{M}^2}=\sqrt{x^2+4^2}\dots \left(1\right)$
Similarly, $ON\mathrm{\perp }CD\Rightarrow CN={\displaystyle \frac{1}{2}}CD={\displaystyle \frac{1}{2}}\times 6=3cm$
Again, $ON\mathrm{\perp }CD$
∴∆OCN is a right triangle with OC=OA (radius of the circle) as hypotenuse.
So, by Pythagoras theorem, we get
$OC=OA=\sqrt{O{N}^2+C{N}^2}=\sqrt{{\left(x+1\right)}^2+3^2}\dots \left(2\right)$
Comparing (1) and (2) we get
$\begin{array}{c}\sqrt{x^2+4^2}=\sqrt{{\left(x+1\right)}^2+3^2}\\ x^2+16=x^2+2x+1+9\\ 2x=16-10\\ 2x=6\\ x=3cm\end{array}$
So, considering ∆OMA
$\mathrm{\angle }OMA={90}^{\circ }$
∴ ∆OMA is a right triangle with OA as hypotenuse.
So, by Pythagoras Theorem, we get
$\begin{array}{c}OA=\sqrt{O{M}^2+A{M}^2}=\sqrt{x^2+4^2}\\ OA=\sqrt{3^2+4^2}\\ OA=\sqrt{9+16}\\ OA=5cm\end{array}$

So, the radius of the given circle is 5 cm.

Note: Some important things should be kept in mind:
1) Chords which are equal in length subtend equal angles at the centre of the circle.
2) If the angles subtended by the chords of a circle are equal in measure, then the length of the chords is equal.
3) Equal chords of a circle are equidistant from the centre of the circle.