
A yo-yo is resting on a perfectly rough horizontal table. Now, forces
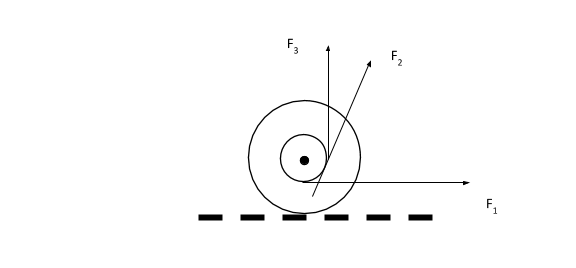
A) When
B) When
C) When
D) When

Answer
504.9k+ views
Hint:The centre of mass of the yo-yo paced on the horizontal surface when a force is applied to it. The direction of motion of the centre of mass will along the direction of the force applied. Here, out of the three forces applied to the yo-yo, only the force
Complete step by step answer.
Step 1: Describe the effect on the centre of mass of the yo-yo when force
The force
Therefore, on the application of the force
Step 2: Describe the effect on the centre of mass of the yo-yo when force
To explain the effect of the force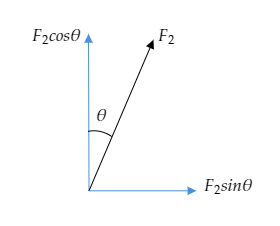
Here, only the horizontal component of
Step 3: Describe the effect on the centre of mass of the yo-yo when force
The force
Therefore, we can conclude that when force
Note: The surface on which the yo-yo resides is described as a perfectly rough horizontal surface. This implies that frictional forces are evident. When force
Complete step by step answer.
Step 1: Describe the effect on the centre of mass of the yo-yo when force
The force
Therefore, on the application of the force
Step 2: Describe the effect on the centre of mass of the yo-yo when force
To explain the effect of the force

Here, only the horizontal component of
Step 3: Describe the effect on the centre of mass of the yo-yo when force
The force
Therefore, we can conclude that when force
Note: The surface on which the yo-yo resides is described as a perfectly rough horizontal surface. This implies that frictional forces are evident. When force
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹33,300 per year
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Trending doubts
1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

How much is 23 kg in pounds class 11 chemistry CBSE

How do I get the molar mass of urea class 11 chemistry CBSE

How do I convert ms to kmh Give an example class 11 physics CBSE

Where can free central placentation be seen class 11 biology CBSE

What is the molecular weight of NaOH class 11 chemistry CBSE




