Question

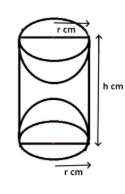
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in figure. If the height of the cylinder is 10cm and its base is of radius 3.5cm, find the total surface area of the article.

Answer 1

Hint: In this question the total surface area of the article will be equal to the curved surface area of the cylinder added with twice the surface area of the hemisphere. Use the direct formula for curved surface area of cylinder and surface area of hemisphere.

Complete step-by-step answer:

Given data
Height (h) of cylinder = 10 cm
And the base radius (r) of the cylinder = 3.5 cm
Now it is given that a wooden article was made by scooping out a hemisphere from each end of a solid cylinder.
So the total surface area (T.S.A) of the article = curved surface area of the cylinder + (2$ \times $surface area of the hemisphere).
Now as we know that the curved surface area of the cylinder is =$2\pi rh$.
And the surface area of the hemisphere =$\left( {2\pi {r^2}} \right)$.
$ \Rightarrow T.S.A = 2\pi rh + \left( {2 \times 2\pi {r^2}} \right) = 2\pi rh + 4\pi {r^2}$ $cm^2$
Now substitute the values in above equation we have,
$ \Rightarrow T.S.A = \left( {2 \times \dfrac{{22}}{7} \times 3.5 \times 10} \right) + \left( {4 \times \dfrac{{22}}{7} \times {{\left( {3.5} \right)}^2}} \right)$
$ \Rightarrow T.S.A = 220 + 154 = 374{\text{ c}}{{\text{m}}^2}$
So this is the required surface area of the article.

Note: The tricky part here is we have added the surface area and not subtracted them although from the first impression it seems that it should be reduced because the scoop is taken out, reason behind that is the surface area(that is the area exposed to outer surrounding) increase due to scoop however the volume would decrease. In general the difference between curved surface area and the total surface area is that T.S.A includes curved surface along with the area of the bases however C.S.A is only the curved surfaces excluding the base area.