Question

A woman pushes a trunk on a railway platform which has a rough surface. She applies a force of $ 100N $ over a distance of $ 10m $ . Thereafter, she gets progressively tired and her applied force reduces linearly with distance to $ 50N $ . The total distance through which the trunk has been moved is $ 20m $ . Plot the force applied by the woman and the frictional force, which is $ 50N $ versus displacement. Calculate the work done by the two forces over $ 20m $ .

Answer 1

Hint To solve this question, we need to plot the two graphs according to the information given in the question. Then the work done by the two forces can be evaluated from these two plots.

Formula Used: The formula used in solving this question is given by
 $ \Rightarrow W = \int\limits_{x1}^{x2} {Fdx} $ , here $ W $ is the work done by the force $ F $ in displacing an object from the position $ x = {x_1} $ to the position $ x = {x_2} $ .

Complete step by step answer
The whole journey of a total distance of $ 20m $ the woman is divided into two parts. The first $ 10m $ distance is covered by applying a constant force of $ 100N $ . The next $ 10m $ distance is covered by applying a linearly varying force which reduces from $ 100N $ to $ 50N $ . So, the plot of the applied force versus displacement is given as

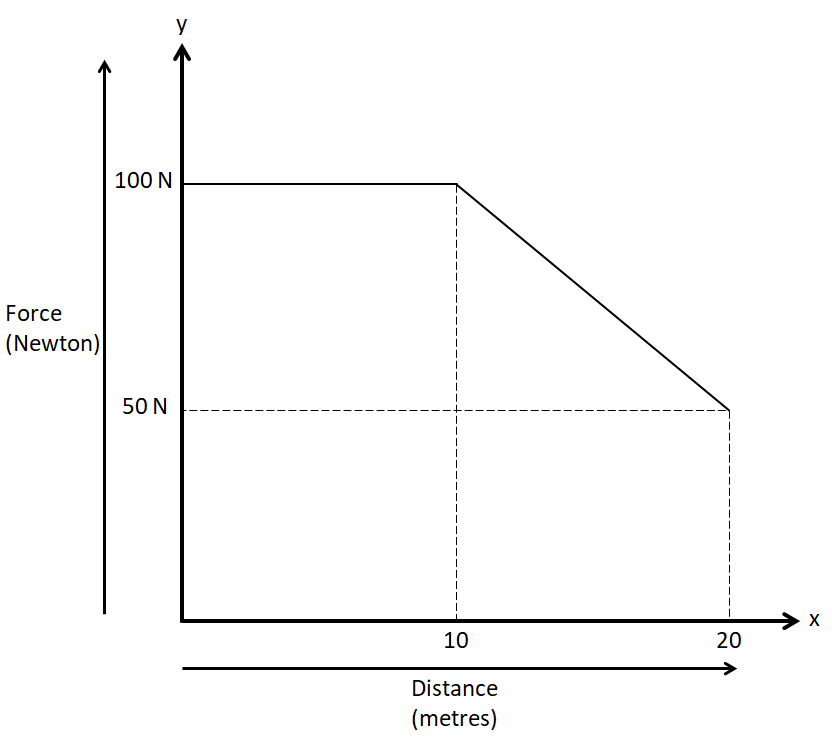
Now, the frictional force is given in the question to be equal to $ 50N $ , which remains constant in the whole journey. It opposes the applied force which is taken as positive. So, the frictional force is taken as negative. The plot of frictional force versus displacement is given as

Hence, the required graphs are plotted.
Now, we know that the work done by a force is given by
 $ \Rightarrow W = \int\limits_{x1}^{x2} {Fdx} $
Since the integration gives the value of the area under the curve between two variables, so the work done by a force is equal to the area under the $ \;F - x $ curve.
Considering the first plot, we get the work done by the applied force as
 $ \Rightarrow {W_F} = {\text{Area of rectangle }} + {\text{ Area of the trapezium }} $
 $ \Rightarrow {W_F} = 100 \times 10 + \dfrac{1}{2}\left( {100 + 50} \right) \times \left( {20 - 10} \right) $
On solving we get
 $ \Rightarrow {W_F} = 1750J $
Now, considering the second plot, we get the work done by the frictional force as
 $ \Rightarrow {W_f} = {\text{Area of rectangle }} $
 $ \Rightarrow {W_f} = - 50 \times 20 $
On solving we get
 $ \Rightarrow {W_f} = - 1000J $ .

Note
You might be wondering as to why the frictional force is constant during the whole journey. This is because, as we know that till there is no relative motion between two surfaces, the force of friction equals the applied force, and remains less than or equal to its maximum value limit. But the trunk in this question is sliding on the rough horizontal surface throughout the whole journey. So the maximum value of friction must be acting on the trunk throughout its motion and hence it is constant.