
A wire is getting elongated by $lmm$ when a load $W$ is hanged from it. When the wire goes over a pulley and two weights $W$ each are hung at the two ends, what will be the elongation of the wire in millimetre?
Answer
556.2k+ views
Hint: At equilibrium, the tension in the wire will be equivalent to the weight of the body or the load hanging on it. The young's modulus can be found by taking the ratio of the weight of the load to the area of cross section which is divided by the ratio of elongated length of the wire to the initial length of the wire. Consider this in both the situations. This will help you in answering this question.
Complete answer:
First of all let us consider the first situation.
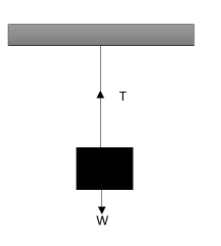
Here at equilibrium, the tension in the wire will be equivalent to the weight of the body or the load hanging on it. Therefore we can write that,
$T=W$
The young's modulus can be found by taking the ratio of the weight of the load to the area of cross section which is divided by the ratio of elongated length of the wire to the initial length of the wire. This can be written as,
$Y=\dfrac{\dfrac{W}{A}}{\dfrac{l}{L}}$
Now in the second situation also, as the load hanging on both the sides are equal, the tension in the wire will be equivalent to the weight of the body hanged.
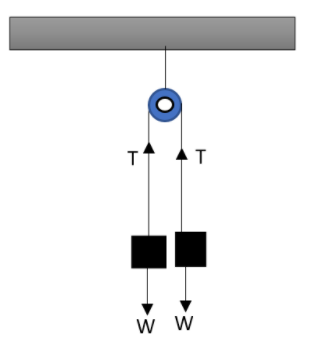
That is,
$T=W$
The young’s modulus for this situation can be written as,
$Y=\dfrac{\dfrac{W}{A}}{\dfrac{l}{L}}$
Therefore the elongation will be the same in both the situations. Hence the elongation of the wire in the second situation will be equivalent to $lmm$.
Note:
The stress in a wire can be found by taking the ratio of the force acting on the wire to the area of the cross section. Strain is another phenomenon occurring which can be found by taking the ratio of the elongated length to the original length. Hence the young’s modulus will be the ratio of the stress to the strain.
Complete answer:
First of all let us consider the first situation.

Here at equilibrium, the tension in the wire will be equivalent to the weight of the body or the load hanging on it. Therefore we can write that,
$T=W$
The young's modulus can be found by taking the ratio of the weight of the load to the area of cross section which is divided by the ratio of elongated length of the wire to the initial length of the wire. This can be written as,
$Y=\dfrac{\dfrac{W}{A}}{\dfrac{l}{L}}$
Now in the second situation also, as the load hanging on both the sides are equal, the tension in the wire will be equivalent to the weight of the body hanged.

That is,
$T=W$
The young’s modulus for this situation can be written as,
$Y=\dfrac{\dfrac{W}{A}}{\dfrac{l}{L}}$
Therefore the elongation will be the same in both the situations. Hence the elongation of the wire in the second situation will be equivalent to $lmm$.
Note:
The stress in a wire can be found by taking the ratio of the force acting on the wire to the area of the cross section. Strain is another phenomenon occurring which can be found by taking the ratio of the elongated length to the original length. Hence the young’s modulus will be the ratio of the stress to the strain.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

Which animal has three hearts class 11 biology CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




