Question

A wire in the form of a rectangle. Its length is 20 cm and breadth is 12cm. If the same wire is rebent in the shape of a square, then what will be the side of the square.

Answer 1

Hint – In this question use the concept that the perimeter of the rectangle will eventually be equal to the perimeter of the square as the rectangle outline wire is reshaped and it’s the same length that has formed the square. So consider the side of the square to be a variable and use this concept to get this variable.

Complete step-by-step answer:

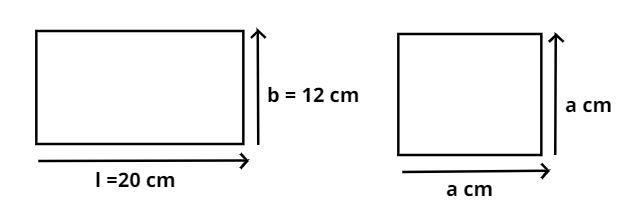
Let the side of the square be a cm.
As the rectangle is reshaped and bent into the square as shown in figure.
Therefore the perimeter of the rectangle is equal to the perimeter of the square.
As we know that the perimeter of any shape is the sum of all the sides.
So the perimeter (P1) of the rectangle is 2(l + b) cm.
Where l and b are the length and breadth of the rectangle respectively.
Now the perimeter (P2) of the square is 2(a + a) = 4a cm.
Where a is the side of the square.
Therefore,
$ \Rightarrow 2\left( {l + b} \right) = 4a$
Now substitute the values in above equation we have,
$ \Rightarrow 2\left( {20 + 12} \right) = 4a$
$ \Rightarrow 4a = 64$
$ \Rightarrow a = \dfrac{{64}}{4} = 16$ cm.
So this is the required side of the square.
So this is the required answer.

Note – It is advised to remember the direct general formula for perimeter, area, C.S.A, T.S.A of basic shapes like rectangle, circle, square etc. as it helps saving a lot of time. There can be another method to find the perimeter of the rectangle instead of using formula $2(l + b)$. We could have used the property that opposite sides of a rectangle are equal and thus the perimeter is simply the sum of all the sides.