Question

A window in a building is at a height of 10 m from the ground. The angle of depression of a point P on the ground from the window is ${{30}^{\circ }}$. The angle of elevation of the top of the building from the point P is ${{60}^{\circ }}$. Find the height of the building.
(a) 30 m
(b) 80 m
(c) 100 m
(d) 50 m

Answer 1

Hint: The building is vertically upright on the ground. Hence, it forms a right angle with the ground. We will use the given information about the angle of depression and angle of elevation to obtain the values of some trigonometric functions at those angles. Using the definition of the trigonometric functions considered, we will be able to establish an equation that will have the height of the building as an unknown variable.

Complete step by step answer:
Let us look at a rough diagram.
 

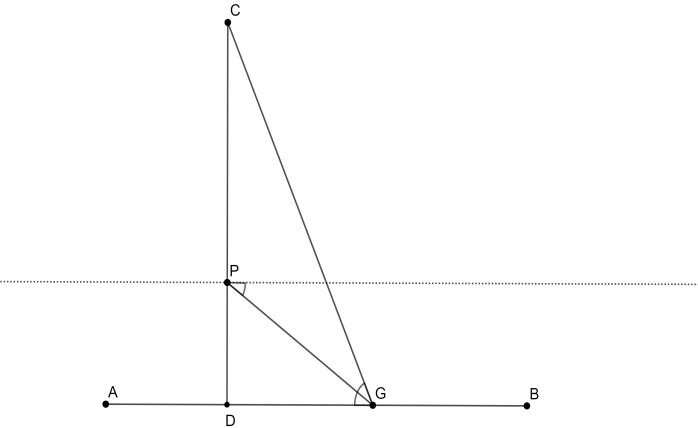
In the figure, segment CD is the building and point P is the window. Therefore, segment PD has length 10 m. The dotted line passing through point P is the horizon. The angle of depression from the window, that is the angle between segment PG and horizon, is ${{30}^{\circ }}$. Since the horizon and the ground are parallel to each other, we can consider segment PG to be a transversal. Therefore, we have $\angle PGD={{30}^{\circ }}$ as they are alternate angles.
Now consider $\Delta PGD$, which is a ${{30}^{\circ }}\text{-}{{60}^{\circ }}\text{-}{{90}^{\circ }}$ triangle. The definition of tan function is given as
$\tan \theta =\dfrac{\text{Opposite}}{\text{Adjacent}}$
We will write tan of ${{30}^{\circ }}$ using the above definition in the following manner,
$\tan {{30}^{\circ }}=\dfrac{PD}{GD}$
We know that $\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$ and $PD=10$. Substituting these values in the above equation, we get
$GD=10\sqrt{3}$
The top of the building is represented by point C. The angle of elevation from point G on the ground to the top of the building is given as ${{60}^{\circ }}$. Now we will consider $\Delta CGD$. This triangle is also a ${{30}^{\circ }}\text{-}{{60}^{\circ }}\text{-}{{90}^{\circ }}$ triangle. In this triangle, we will write tan of ${{60}^{\circ }}$ using the definition as follows,
$\tan {{60}^{\circ }}=\dfrac{CD}{GD}$
We know that $\tan {{60}^{\circ }}=\sqrt{3}$ and $GD=10\sqrt{3}$. Substituting these values in the above equation, we get
$CD=10\sqrt{3}\times \sqrt{3}=30$
Therefore, the height of the building is 30 m.

So, the correct answer is “Option A”.

Note: It is useful to draw diagrams in such types of questions. Looking at the diagram, it is easier to make a choice for the trigonometric function to be used. It is useful to know the values of the trigonometric functions for standard angles.