Question

A wheel with 8 metallic spokes each 50cm long is rotated with the speed of $120rev/\min$ in a plane normal to the horizontal component of the earth's magnetic field. The earth’s magnetic field at the place is $0.4G$ at an angle of ${60^0}$. Calculate the EMF induced between the axle and the rim of the wheel. How will the value of EMF be affected if the number of spokes was increased?

Answer 1

Hint: The induced emf in a rod rotating in a magnetic field is given by $E = \dfrac{1}{2}B\omega {L^2}$. First, we have to find the emf induced in one spoke of the wheel due to the magnetic field. Then we find the resultant emf of all the spokes.

Complete answer:

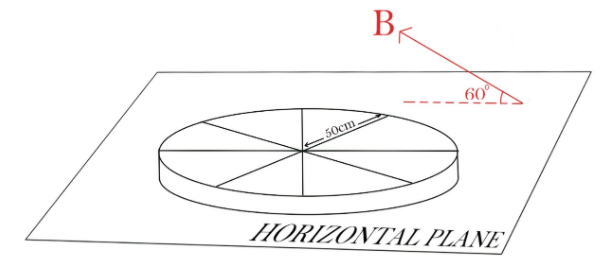
It is given in the question that the horizontal component of the earth’s magnetic field is making an angle of ${60^0}$.
So, the component of magnetic field which is in the plane of wheel
$ = 0.4\cos {60^0}$
We know that $cos {60^0}=\dfrac{1}{2}$
$
= 0.4 \times \dfrac{1}{2} \\
= 0.2G \\
 $
We know that, $1G = {10^{ - 4}}T$ So,
$B = 0.2 \times {10^{ - 4}}T$
Now,
We will find the Emf by one rod,
Emf induces in a rod of length L and rotating with angular speed $\omega $is given by the formula
$E = \dfrac{1}{2}B\omega {L^2}$
Where,
$\omega = $angular velocity of the rod
$B = $external magnetic field
$L = $length of the rod
Also,
Angular velocity is the ratio of angular displacement to time,
$\omega = \dfrac{{2\pi n}}{t}$
Substituting the value of $\omega $in the formula we get,
$\Rightarrow E = \dfrac{{B{L^2}\pi n}}{t}$
$\Rightarrow E = \dfrac{{0.2 \times {{10}^{ - 4}} \times {{0.5}^2} \times 3.14 \times 120}}{{60}}$
On simplifying the above terms, we get
$\Rightarrow E = 3.14 \times {10^{ - 5}}V$

$\therefore$ This is the emf produced by one spoke of the wheel. All the eight spokes of the wheel are connected in parallel to each other. This is because one end of each spoke is connected to every other spoke directly and the other end of each spoke is connected to the same rim itself. So we can imagine all the spokes in which emf is induced to be parallel with each other. We know that, if n number of cells are connected in parallel with each other then the net emf remains the same. So, no change in emf will remain unchanged on increasing the spokes in the wheel.

Note:
The rotating rods can be considered as a cell and all the cells will have the same polarity because all the rods are rotating in the same sense. To solve these kinds of questions, you have to picturise the given information and clearly understand the direction of the magnetic field.