Question

A wheel of radius $R$ is rolling inside a fixed circular cylinder of radius $2R$ as shown. What is the trajectory followed by a point on the rim of the wheel:-

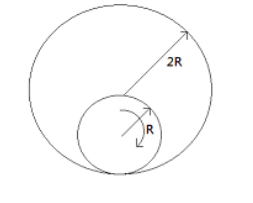
A) Circle
B) Cycloid
C) Straight line
D) None of these

Answer 1

Hint:For easy calculation, consider the inner wheel is rolling on a surface with length equal to the circumference of the circle of circular cylinder. It would then be easy to imagine the trajectory of a point on the wheel. After obtaining the trajectory, place the same trajectory in the circular cylinder.

Complete step by step solution:We have to find the trajectory of a point on the wheel, while it is rolling inside the cylinder. We can assume the wheel has moved some angular displacement and then we can find that angular displacement using trigonometry and integrate that angular displacement for ${360^ \circ }$ .

The easier approach would be to assume the wheel rolling on a horizontal surface having length equal to the circumference of the circular cylinder. The path traced by a point in such a case is depicted in the below figure.

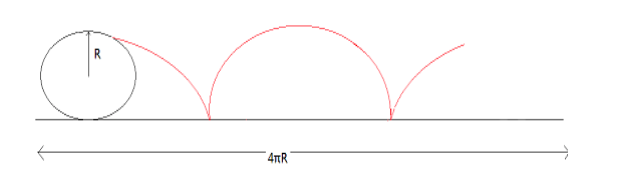
Now when again, when we enclose the linear horizontal path in the form of a circular cylinder. The shape obtained will be as follows:

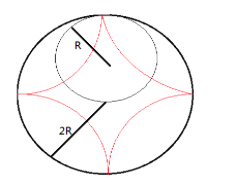
The curve drawn in red color is the path followed by the inner wheel when it rolls inside the circular cylinder. This shape is cycloid.

Therefore, option B is the correct answer.

Note:It is easier to imagine the path followed once the problem is converted into some other example which we are aware of. It is difficult to imagine and draw the path inside. Don’t confuse cycloids with circles.