Question

A wheel of radius R and mass M is placed at the bottom of a fixed step of height R as shown in the figure. A constant force is continuously applied on the surface of the wheel so that it just climbs the step without slipping. Consider the torque $\tau $ about an axis normal to the plane of the paper passing through the point Q. Which of the following options is/are correct?

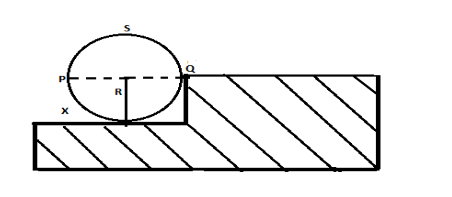
1) If the force is applied tangentially at point s $\tau $$ \ne $ 0 but the wheel never climbs the step.
2) If the force is applied normal to the circumference at point P then $\tau $= 0.
3) If the force is applied normal to the circumference at point X then $\tau $= constant.
4) If the force is applied normal to the circumference at point P tangentially then $\tau $decreases continuously as the wheel climbs.

Answer 1

Hint: For the question above we will use the concept which gives the equation of torque as:
$\tau = F \times r \times \sin \theta $ (F is the force, r is the distance between the axis of rotation and the point where the force happens, $\tau $ is the torque and $\theta $ is the angle between the direction of the force and the line that joins the axis to the point.)
We also make use of:
$F = ma$
Complete step by step solution:
Let’s discuss a few points which that at what conditions the torque is zero and what torque is:
Torque is simply a force but instead of making the object to move it makes the object to spin.

When force applied on an object is zero then torque is also zero. When a number of forces are acting on a body and cancels each force, then also torque becomes zero. If the force acts on the axis of rotation, torque will become zero. When the force goes towards the axis of rotation, it makes torque zero.
Now, we will discuss each option given in the question and select the most appropriate option.
-If the force is applied tangentially at point s $\tau $$ \ne $ 0 but the wheel never climbs the step. When $\tau $is not zero and the force is applied tangentially the wheel must climb because when torque is there some spin must take place to the wheel. Therefore this option is not correct. According to the relation$\tau = F \times r \times \sin \theta $ all the conditions for torque to exist.
-If the force is applied normal to the circumference at point P then $\tau $= 0.when force distance of axis R and $\theta $ is equal to zero then torque will also be zero. $\tau = F \times r \times \sin \theta $ at $\theta $is equal to zero sin$\theta $ will be zero and hence torque will be zero. Option is correct.
-If the force is applied normal to the circumference at point X then $\tau $= constant. When the force is applied at point X distance will become 2r, force will make some angle $\theta $with 2r and hence the torque will be constant option is correct.
-If the force is applied normal to the circumference at point P tangentially then $\tau $decreases continuously as the wheel climbs. When force is applied tangentially at point P then force vector and 2r will make some angle $\theta $ and the torque will be constant. No decrease in torque will take place when the wheel will climb.
Option 2 and 3 are correct.

Note: We have a number of applications where we find torque is applied such as a door bolted at one end with the hinges when the force door gets opened or closed with some angle of movement, and at the distance equal to the distance between the hinges of the door and our hand.