Question

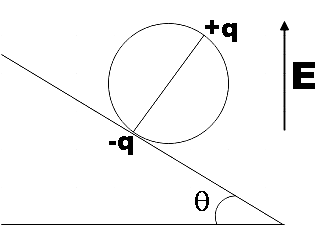
A wheel having mass m has charges +q and –q on diametrically opposite points. It remains in equilibrium on a rough inclined plane in the presence of a vertical electric field E. Then value of E is:

A. $\dfrac{mg\tan \theta }{q}$
B.$\dfrac{mg}{q}$
C. $\dfrac{mg}{2q}$
D. $\dfrac{mg\tan \theta }{2q}$

Answer 1

Hint: As it is said that the wheel is in equilibrium position on the incline, it would directly imply that the net torque on it is zero. Now you could find all the possible torques acting on the wheel. There will be one due to the dipole and other due to the frictional force. Then, you could equate their sum to zero and rearrange to get the value of the electric field.

Formula used: Torque,
$\tau =PE\sin \theta $
$\tau =F\times r$

Complete step by step answer:
In the question we are given a wheel of mass m kept on a rough inclined plane in the presence of electric field E. This wheel has charges +q and –q kept at its diametrically opposite points. We are also said that this wheel remains in equilibrium and is asked to find the value of electric field E.
As a first step you could draw a free body diagram.

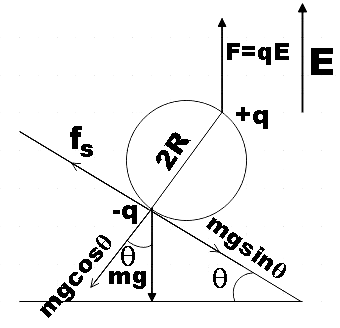
We know that a system containing two equal and opposite charges separated by a distance $a$is called a dipole and the expression for dipole moment in the given situation could be given by,
$P=2Rq$ ………………………. (1)
We know that torque produced due to a dipole is given by,
$\tau =PE\sin \theta $
Substituting (1),
${{\tau }_{1}}=2RqE\sin \theta $ ………………………………… (2)
From the free body diagram we see that the frictional force is equal to the sine component of mg. That is,
${{f}_{s}}=mg\sin \theta $ ………………………… (3)
We know that torque produced by force F is given by,
$\tau =F\times r$
Where r is the perpendicular distance from the center of the body to the point at which the force is acting. So, the torque produced by the frictional force can be found by substituting (3) here.
${{\tau }_{2}}=mg\sin \theta R$ ……………………………….. (4)
As the wheel is in equilibrium, the net torque on it is zero. So the net torque,
${{\tau }_{net}}={{\tau }_{1}}+{{\tau }_{2}}=0$
Substituting (2) and (4),
$2RqE\sin \theta +\left( -mg\sin \theta R \right)=0$
Negative symbol used because of direction.
$\Rightarrow 2RqE\sin \theta =mgR\sin \theta $
$\therefore E=\dfrac{mg}{2q}$
Therefore, we found the value of electric field to be,
$E=\dfrac{mg}{2q}$

So, the correct answer is “Option C”.

Note: You may have noted that we have given a negative sign for the torque caused by frictional force. This is to indicate that the torque produced by frictional force is opposite to that caused by dipole. From the figure, we see that the torque caused by the dipole is in an anticlockwise direction and that by frictional force is in clockwise direction.