Question

a) What are the characteristics of an image formed by a plane mirror?
(b) By giving sign conventions made, derive the mirror formula for a concave mirror.

Answer 1

Hint: Draw the correct ray diagram for both the problems and determine the nature of the image. Find the relative position, shape, and direction of the image. For finding the concave mirror formula, find the similar triangles and compare the sides. Use the appropriate sign conventions for the sides.

Complete step by step answer:
(A) Let’s look at the ray diagram for the plane mirror:

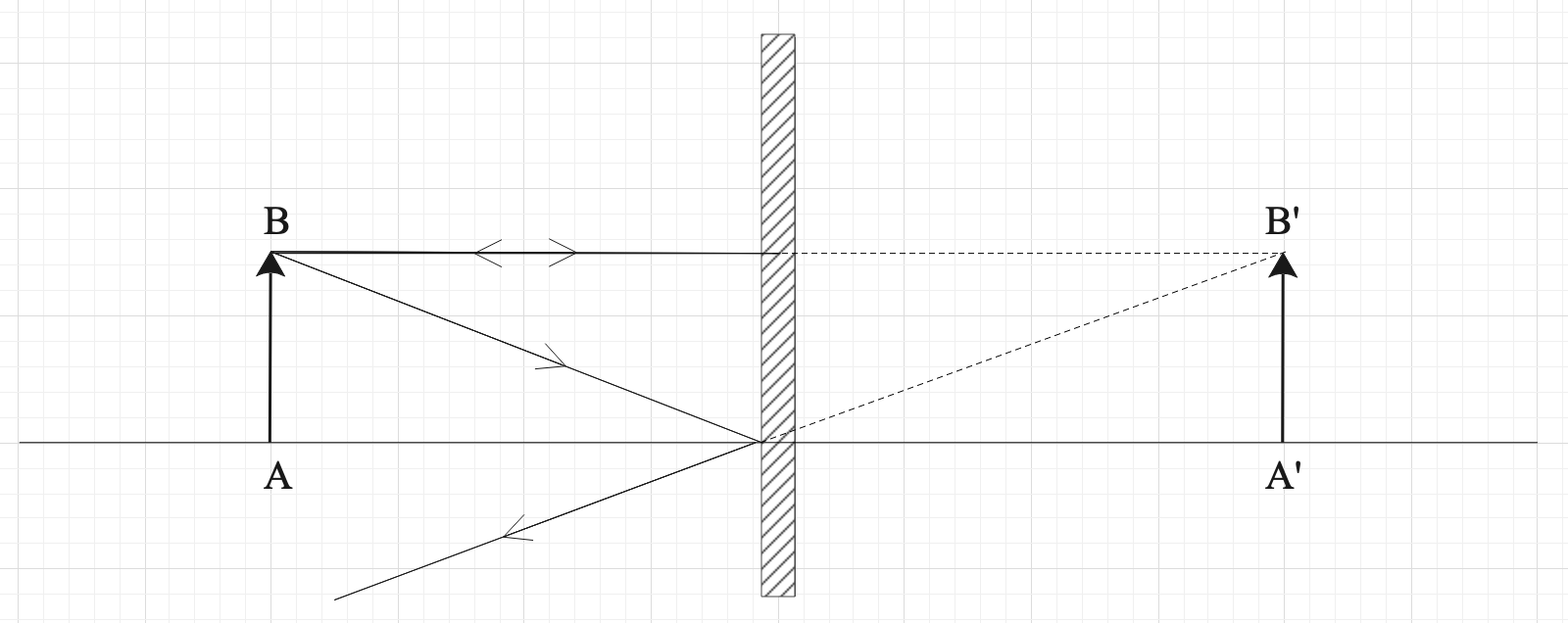
It is quite apparent from the ray diagram that the image produced by a plane mirror is erect, virtual, and has unit magnification.

It also has lateral inversion.


(B) We should start the derivation by drawing a clear ray diagram of the concave mirror.

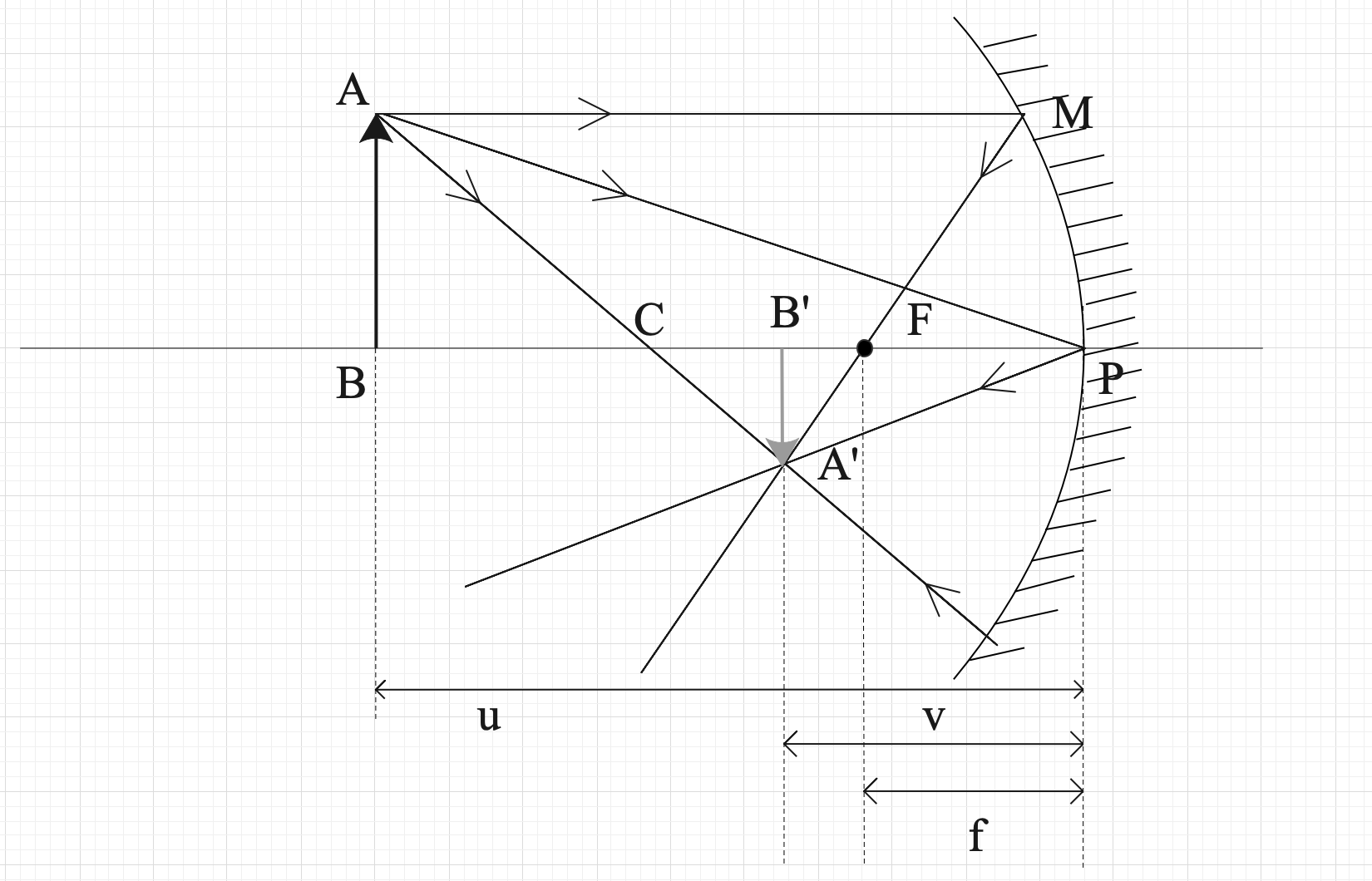
An object AB is kept at a distance of u from the pole of the concave mirror.

The image A’B’ is formed at a distance of v from the pole of the concave mirror.

The focal length of the concave mirror is at a distance of f from the concave mirror.

Sign Convention: Any point which is at the left of the pole of the concave mirror is considered to be negative.

So, we can write the following,

BP = -u, B’P=-v, and FP=-f
Now, we can proceed to the derivation,

For the paraxial ray, we can consider MP to be a straight line, and MPF is forming a right-angled triangle.

Hence, we can consider triangles A’B’F and MPF to be two similar right-angled triangles.

So, we can write,
$\dfrac{B'A'}{PM}=\dfrac{B'F}{FP}$ or, $\dfrac{B'A'}{BA}=\dfrac{B'F}{FP}$.........................(1)
ABP and A’B’P’ are also similar triangles, because,
$\angle APB=\angle A'PB'$

Hence, we can write,
$\dfrac{B'A'}{BA}=\dfrac{B'P}{BP}$.........................(2)


Comparing equation (1) and (2), we get,
$\dfrac{B'F}{FP}=\dfrac{B'P-FP}{FP}=\dfrac{B'P}{BP}$........................(3)
If we put the sign conversion, in the equation (3) we get,
$\dfrac{-v+f}{-f}=\dfrac{-v}{-u}$
$\Rightarrow \dfrac{v-f}{f}=\dfrac{v}{u}$
$\Rightarrow \dfrac{1}{v}+\dfrac{1}{u}=\dfrac{1}{f}$

So, the mirror formula is,
$\dfrac{1}{v}+\dfrac{1}{u}=\dfrac{1}{f}$

Note: You need to remember the sign convention that we have mentioned. It is very important that you follow a specific sign convention while solving optics problems. This will make sure that you don’t commit unnecessary mistakes.
If we follow the same procedure, we can find the same mirror formula for the convex mirror as well. However, we need to follow the sign conversion according to the convex mirror.