Question

A well with inner diameter 8 m is dug 14 m deep Earth taken out it has been spread evenly all around it to a width of 3 m to form an embankment around the well, then the height of this embankment is
(a) $6\dfrac{26}{33}m$
(b) $7\dfrac{26}{33}m$
(c) $4\dfrac{26}{33}m$
(d) $5\dfrac{26}{33}m$

Answer 1

Hint: We start solving the problem by drawing the figure representing given information. We then find the volume of the material from the well by using the fact that the volume of the circular solid cylinder with diameter ‘d’ and height ‘h’ is $\dfrac{\pi {{d}^{2}}h}{4}$. We then assume the height of the embankment and then find the volume of it by using the fact that the volume of the hollow cylinder with inner diameter ${{d}_{1}}$, outer diameter ${{d}_{2}}$ and having height h is $\dfrac{\pi }{4}\left( d_{2}^{2}-d_{1}^{2} \right)h$. We then equate both the obtained volumes and then make the necessary calculations to get the required value of height of embankment.

Complete step by step answer:
According to the problem, we are given that well with an inner diameter 8 m is dug 14 m deep Earth taken out it has been spread evenly all around it to a width of 3 m to form an embankment around the well and we need to find the height of the embankment.
Let us draw the figure representing the given information.

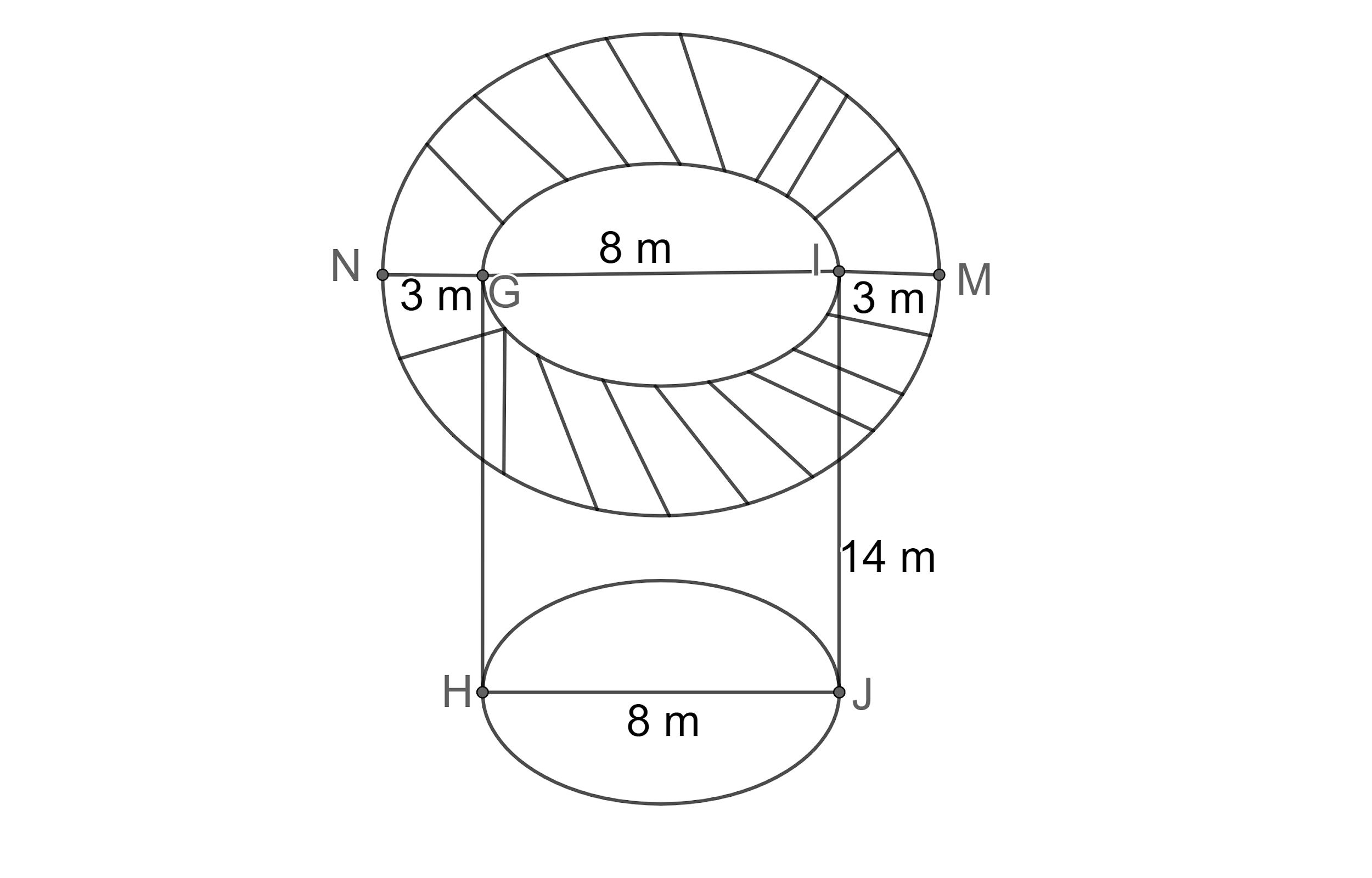
The shaded region is where embankment of material is done.
Let us find the volume of the material removed due for digging the well.
From the figure, we can see that well GHJI resembles a circular cylinder with diameter 8m and height 14 m.
We know that the volume of the circular solid cylinder with diameter ‘d’ and height ‘h’ is $\dfrac{\pi {{d}^{2}}h}{4}$.
So, the volume of the material removed is ${{V}_{R}}=\dfrac{\pi {{\left( 8 \right)}^{2}}\left( 14 \right)}{4}=224\pi {{m}^{3}}$ ---(1).
Let us assume the height of the embankment is ‘h’ m.
Now, let us find the volume of the embankment. From the figure, we can see that the embankment resembles a hollow cylinder with inner diameter 8m and outer diameter as $\left( 8+3+3 \right)=14m$.
We know that the volume of the hollow cylinder with inner diameter ${{d}_{1}}$, outer diameter ${{d}_{2}}$ and having height h is $\dfrac{\pi }{4}\left( d_{2}^{2}-d_{1}^{2} \right)h$.
So, we get the volume of embankment as ${{V}_{E}}=\dfrac{\pi }{4}\left( {{14}^{2}}-{{8}^{2}} \right)h$.
$\Rightarrow {{V}_{E}}=\dfrac{\pi }{4}\left( 196-64 \right)h$.
$\Rightarrow {{V}_{E}}=\dfrac{\pi }{4}\left( 132 \right)h$.
$\Rightarrow {{V}_{E}}=\left( 33\pi h \right){{m}^{3}}$ ---(2).
From the problem, we are given that the embankment is made with the material dug for well. So, we get ${{V}_{R}}={{V}_{E}}$.
$\Rightarrow 224\pi =33\pi h$.
$\Rightarrow h=\dfrac{224\pi }{33\pi }$.
$\Rightarrow h=\dfrac{224}{33}$.
$\Rightarrow h=\dfrac{198+26}{33}$.
$\Rightarrow h=5+\dfrac{26}{33}$.
$\Rightarrow h=5\dfrac{26}{33}$.

So, the correct answer is “Option d”.

Note: We can see that the given problem contains a huge amount of calculation, so we need to perform each step carefully in order to avoid calculation mistakes. We should not confuse formulas of volumes of hollow cylinder and solid cylinder while solving this problem. We should not make mistakes while converting the obtained answer into mixed fractions. Similarly, we can expect problems to find the width of the embankment if the height is 6m.