Question

A well of diameter $7m$ and $30m$ deep is dug and the soil obtained by digging
 the well is evenly spread out to form a platform of size $30m\times 10m$. Find the height of
 the platform.

Answer 1

Hint: Use the basic definition of volume. As we can relate that if we dug soil with
 $7m$ diameter and $30m$ deep, then it is termed as well but if we observe it geometrically
 then it is of the cylindrical shape which has some given height and diameter.

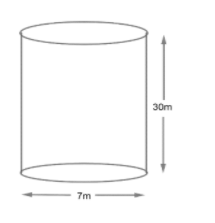
The soil present inside the well (dug out) represents the volume of the cylinder as we are
 talking about the quantity part of the cylinder.
Hence, soil dug out$=$ volume of cylinder or well $=\pi {{R}^{2}}H$(Formula to calculate
 volume of cylinder)
Where, $R=$ radius of cylinder
$H=$ Height of cylinder
$\pi =\dfrac{22}{7}$
Soil dug out of well $=\dfrac{22}{7}{{\left( \dfrac{7}{2} \right)}^{2}}\times 30$
$\because $ radius $=$ diameter
$\dfrac{-r}{2}$
$\begin{align}
  & =\dfrac{22}{7}\times \dfrac{49}{4}\times 30 \\
 & =22\times 7\times \dfrac{15}{2}=77\times 15 \\
\end{align}$
Soil dug out $=1155{{m}^{3}}.................\left( i \right)$
Now, as discussed in the question that the soil dug out from the well is transformed to
 platform I form of cuboid which has some height, width and length.

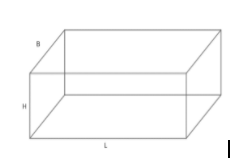
From the question we have
$\begin{align}
  & L=30m \\
 & B=10m \\
 & H=? \\
\end{align}$
(Need to calculate)
Now, we can relate from the above information that soil dug out from the cylinder is
 converted in the shape of a cuboid; and as we have already discussed that soil represents
 quantity which is getting converted from one form to another quantity will remain constant
 whatever the shape would be.
Now, let us calculate volume of cuboid/platform
$V=length\times breadth\times height$
From the given information in question:
$\begin{align}
  & L=30m \\
 & B=10m \\
 & H=? \\
\end{align}$
$\begin{align}
  & V=30\times 10\times H \\
 & V=300H{{m}^{3}}..............\left( ii \right) \\
\end{align}$
As we have related already that
Volume of well $=$ Volume of platform
Hence, from the equation (i) and (ii)
\[\begin{align}
  & 300H=1155 \\
 & H=\dfrac{1155}{300} \\
 & H=\dfrac{385}{100}=3.85m \\
\end{align}\]
Hence, height of platform $=3.85m$
Note: One can relate the surface areas (total/curved) between cylinder/well and platform/cuboid, but that will give the wrong answer because quantity is not represented by area of any geometrical shape. Area represents the amount of space enclosed whereas volume determines the capacity of solids.Hence, we need to take care of it.