Question

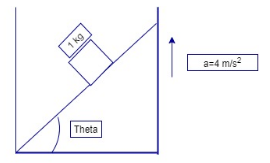
A wedge is moving with an acceleration a= $ 4\text{m/}{{\text{s}}^{2}} $ vertically up as shown in figure. What is acceleration of block of mass $ 1\text{kg} $ w.r.t wedge normal reaction by wedge on block respectively. All surfaces are smooth. Choose correct pair $ \left( \text{g=10m/}{{\text{s}}^{2}} \right) $

(A) $ 7\text{ m/}{{\text{s}}^{2}},7\sqrt{3}\text{ N} $
(B) $ \text{5 m/}{{\text{s}}^{2}},5\sqrt{3}\text{ N} $
(C) $ 4\cdot 9\text{ m/}{{\text{s}}^{2}},\text{ 4}\cdot \text{9}\sqrt{3}\text{ N} $
(D) $ \text{10 m/}{{\text{s}}^{2}},10\sqrt{3}\text{ N} $

Answer 1

Hint: The magnitude of the force of limiting friction between any two bodies in constant is directly proportional to the normal reaction between them. Direction of the force of limiting friction is always opposite to the direction in which one body is at the verge of moving over the other.
Limiting friction: Is the maximum opposing force that comes into play, when one body is just at the verge of moving over the surface of the other body.

Complete step by step solution
A wedge is moving in upward direction with acceleration $ 4\text{ m/}{{\text{s}}^{2}} $ . A block is placed on the wedge having mass ‘m’.

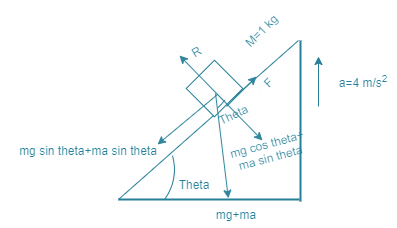
The various forces involved are:
Weight, mg of the body, acting vertically downwards.
Normal reaction, R, acting perpendicular to the inclined plane of wedge.
Force of friction, F acting up the plane.
Now, mg can be resolved into two rectangular components:
mg $ \text{cos }\!\!\theta\!\!\text{ } $ opposite to R
mg $ \text{sin }\!\!\theta\!\!\text{ } $ opposite to F
As the wedge is accelerated in upward direction with acceleration, then the Pseudo force will act on the body. It is the product of the mass of the body and acceleration. i.e.
F=ma
In the frame of wedge:
Horizontal component:
Left side forces=Right sides forces
mg $ \text{sin }\!\!\theta\!\!\text{ }+ $ ma $ \text{sin }\!\!\theta\!\!\text{ } $ =ma
In this a= acceleration of wedge
$ {{\text{a}}_{1}} $ =according of Bex
 $ \begin{align}
  & \text{mg}\left( \text{g}+\text{a} \right)\sin \text{ }\!\!\theta\!\!\text{ }=\text{m }{{\text{a}}_{1}} \\
 & {{\text{a}}_{1}}=\left( \text{g}+\text{a} \right)\sin \text{ }\!\!\theta\!\!\text{ } \\
 & =\left( 10+4 \right)\sin 30 \\
 & =14\times \dfrac{1}{2} \\
 & =7\text{ m/}{{\text{s}}^{2}} \\
\end{align} $
To find out the normal reaction vertically upward force is balanced by velocity downward force.

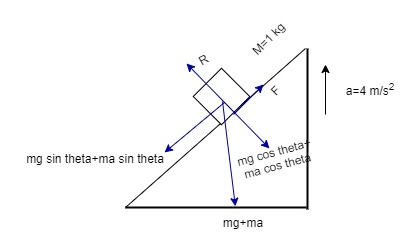
 $ \begin{align}
  & \text{R=mg cos }\!\!\theta\!\!\text{ }+\text{ma cos }\!\!\theta\!\!\text{ } \\
 & =\text{m}\left( \text{g}+\text{a} \right)\text{cos }\!\!\theta\!\!\text{ } \\
 & =1\left( 10+4 \right)\text{cos 30} \\
 & \text{=14}\times \sqrt{3} \\
 & =7\sqrt{3}\text{ N} \\
\end{align} $
Therefore, acceleration of block w.r.t to wedge is $ 7\text{ m/}{{\text{s}}^{2}} $ and normal wedge on block is $ 7\sqrt{3}\text{ N} $
So option (A) is correct answer.

Note
Remember that friction is always opposed to relative motion. Angle of repose is defined as the minimum angle of inclination of a plane with the horizontal, such that a body placed on the plane just begins to slide down. Friction is a non-conservation force i.e. work done against friction is path dependent.