Question

A vessel in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemispherical portion of the vessel is 14cm, and the total height of the vessel is 13cm. Find the inner surface area of the vessel.
[a] 557 square centimetres
[b] 517 square centimetres
[c] 537 square centimetres
[d] 572 square centimetres

Answer 1

Hint: Assume that the height of the cylindrical part is h. Observe that the total height of the object is the sum of the height of the cylinder and the radius of the hemisphere. Hence determine the height of the cylinder. Use the fact that the curved surface area of a cylinder $=\pi {{r}^{2}}h$ and the curved surface area of the hemisphere $=2\pi {{r}^{2}}$. Hence determine the inner surface area of the vessel.

Complete step-by-step answer:

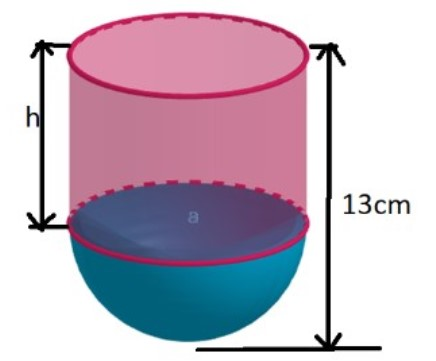
We have the diameter of the hemisphere = 14cm.
Hence the radius of the hemisphere $=\dfrac{14}{2}=7cm$.
Hence the radius of the hemisphere = 7cm
Let the height of the cylinder be h. As is evident from the diagram above, the height of the vessel is the sum of the height of the cylinder and radius of the hemisphere.
Hence, we have
h+7 = 13
Subtracting 7 from both sides, we get
h = 6
Hence the height of the cylinder = 6cm.
Now, we know that the curved surface area of a cylinder $=\pi {{r}^{2}}h$ and the curved surface area of the hemisphere $=2\pi {{r}^{2}}$
Hence, the inner surface area of the vessel $=\pi {{r}^{2}}+2\pi rh=2\pi r\left( h+r \right)=2\times \dfrac{22}{7}\times 7\times \left( 6+7 \right)=572$
Hence, the inner surface area of the vessel = $572cm^{2}$.
Hence option [d] is correct.

Note: In the above question, students usually make a mistake in taking the height of the cylinder. The height of the cylinder, in this case, is not equal to the height of the vessel.The total height of the object is the sum of the height of the cylinder and the radius of the hemisphere.