Question

A vertical wall of height running from south to north has a height. A policeman of height b > a is standing in front of the wall at a distance c from it on the eastern side. What should be the maximum distance of a crawling thief from the wall so that the thief can hide from the view of the policeman if the thief is on the other side of the wall in the west of the policeman?
a) $\dfrac{ac}{b-a}$
b) $\dfrac{bc}{b-a}$
c) $\dfrac{a+b}{b-a}.c$
d) $\dfrac{ac}{b-a}$

Answer 1

Hint: Let us assume that the distance of a crawling thief from wall is x in the west direction. So, we gathered two triangles. Now, by using the similarity of triangles, find the value of x.

Complete step by step answer:

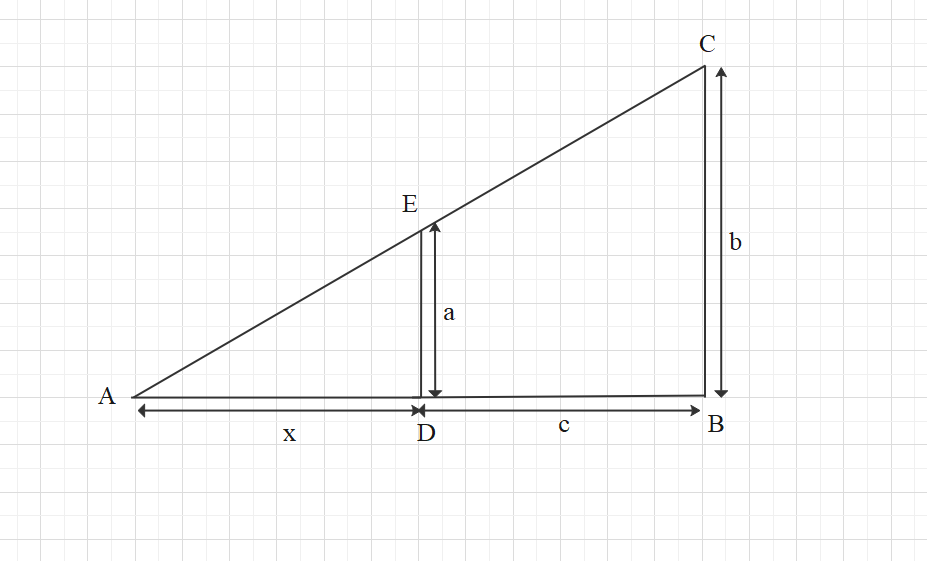
We have:
Height of wall: DE = a
Height of policeman: BC = b
Distance of policeman from wall: BC = c
Now, we have two triangles as: $\Delta ABC$ and $\Delta ADE$
In $\Delta ABC$ and $\Delta ADE$
Since, $DE\parallel BC$
Therefore, $\angle ADE=\angle ABC$ and $\angle AED=\angle ACB$ (alternate interior angles)
So, $\Delta ABC\approx \Delta ADE$ ( by AAA similarity)
Therefore, we can say that:
$\dfrac{AD}{AB}=\dfrac{DE}{BC}=\dfrac{AE}{AC}$
So, we have:
$\begin{align}
  & \Rightarrow \dfrac{AD}{AB}=\dfrac{DE}{BC} \\
 & \Rightarrow \dfrac{AD}{AD+DB}=\dfrac{DE}{BC} \\
 & \Rightarrow \dfrac{x}{x+c}=\dfrac{a}{b} \\
\end{align}$
So, by solving the above equation, we get:
$\begin{align}
  & \Rightarrow bx=a\left( x+c \right) \\
 & \Rightarrow bx-ax=ac \\
 & \Rightarrow x\left( b-a \right)=ac \\
 & \Rightarrow x=\dfrac{ac}{b-a} \\
\end{align}$

So, the correct answer is “Option D”.

Note:
Two triangles are said to be similar if
a) Their corresponding angles are equal, and
b) Their corresponding sides are proportional.