Question

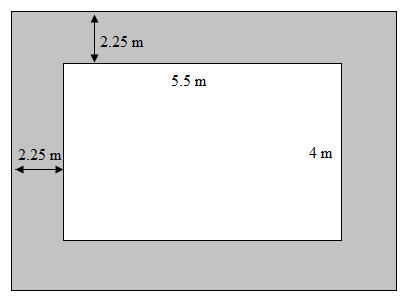
A verandah of width \[2.25\] m is constructed all along outside a room which is \[5.5\] m long and 4 m wide. Find the area of the verandah.

Answer 1

Hint:
Here, we need to find the area of the verandah. The area of the verandah is the difference in the areas of the two rectangles. We will use the formula for the area of a rectangle to find the two areas. Then subtract the area of the smaller rectangle from the area of the bigger rectangle to find the required area of the verandah.

Formula Used:
We will use the formula Area of rectangle \[ = l \times b\], where \[l\] is the length of the rectangle and \[b\] is the breadth of the rectangle.

Complete Step by Step Solution:
From the figure, we can observe that the area of the verandah is the difference in the area of the bigger rectangle and the smaller rectangle.
First, we will calculate the area of the smaller rectangle.
The area of a rectangle is the product of its length and breadth.
Substituting the length as \[5.5\] m, and the breadth as 4 m in the formula Area of rectangle \[ = l \times b\], we get
Area of the smaller rectangle \[ = 5.5 \times 4{\rm{ }}{{\rm{m}}^2}\]
Multiplying the terms in the expression, we get
\[ \Rightarrow \] Area of the smaller rectangle \[ = 22{\rm{ }}{{\rm{m}}^2}\]
Thus, we get the area of the smaller rectangle as 22 square metres.
Now, we will calculate the area of the bigger rectangle.
The verandah is \[2.25\] m wide.
The length of the bigger rectangle is the sum of the length of the smaller rectangle, and twice the width of the verandah.
Thus, we get
Length of the bigger rectangle \[ = 5.5 + 2\left( {2.25} \right)\]
Multiplying the terms in the expression, we get
\[ \Rightarrow \] Length of the bigger rectangle \[ = 5.5 + 4.5\]
Adding the terms, we get
Length of the bigger rectangle \[ = 10\] m
Similarly, the breadth of the bigger rectangle is the sum of the breadth of the smaller rectangle, and twice the width of the verandah.
Thus, we get
Breadth of the bigger rectangle \[ = 4 + 2\left( {2.5} \right)\]
Multiplying the terms in the expression, we get
\[ \Rightarrow \] Breadth of the bigger rectangle \[ = 4 + 4.5\]
Adding the terms, we get
Breadth of the bigger rectangle \[ = 8.5\] m
Substituting the length as 10 m and the breadth as \[8.5\] m in the formula for area of a rectangle, we get
Area of the bigger rectangle \[ = 10 \times 8.5{\rm{ }}{{\rm{m}}^2}\]
Multiplying the terms in the expression, we get
\[ \Rightarrow \] Area of the bigger rectangle \[ = 85{\rm{ }}{{\rm{m}}^2}\]
Thus, we get the area of the bigger rectangle as 85 square metres.
Finally, we can calculate the area of the verandah.
The area of the verandah is the difference in the area of the bigger rectangle and the smaller rectangle.
Therefore, we get
Area of the verandah \[ = 85{\rm{ }}{{\rm{m}}^2} - 22{\rm{ }}{{\rm{m}}^2}\]
Subtracting the terms in the expression, we get
\[ \Rightarrow \] Area of the verandah \[ = 63{\rm{ }}{{\rm{m}}^2}\]

Therefore, we get the area of the verandah as 63 square metres.

Note:
A common mistake is to calculate the length of the bigger rectangle as the sum of the length of the smaller rectangle, and the width of the verandah, that is \[5.5 + 2.25 = 7.75{\rm{ m}}\]. This is incorrect, because the verandah is constructed around all the sides of the smaller rectangle. Therefore, the length of the smaller rectangle is increased by \[2.25\] m from both left and right side to get the length of the bigger rectangle. Similarly, the breadth of the bigger rectangle is calculated.