Question

A verandah 1.25 m is constructed all along outside of a room 7.5 m long and 5 m wide. Find
(i) the area of the verandah.
(ii) the cost of cementing the floor of the verandah at the rate of Rs.15 per $m^{2}$.

Answer 1

Hint: In this question it is given that a verandah 1.25 m is constructed all along outside of a room 7.5 m long and 5 m wide. We have to find the area of verandah and the cost of cementing the floor of the verandah at the rate of Rs.15 per $m^{2}$. So for this we need to draw the diagram,

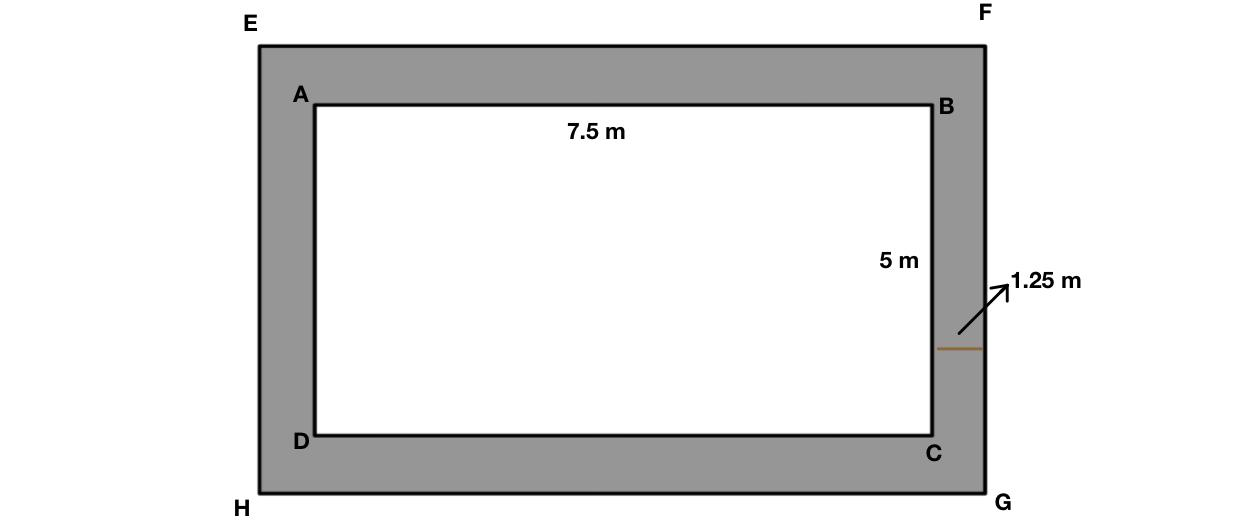
In the diameter the shaded portion is the verandah, so to find the solution we need to know the formula of area of a rectangle, A=$$\text{length} \times \text{width}$$.....(1)
And the area of the verandah = (area of EFGH) - (area of ABCD)

Complete step-by-step answer:
Given, the length of the room = AB=DC=7.5 m
And the width=AD=BC=5 m
Therefore the area of ABCD=$AB\times AD$=$7.5\times 5\ m^{2}$=$37.5 m^{2}$
Now since, verandah 1.25 m is constructed all along outside of a room ABCD,
So the rectangular boundary including the verandah is EFGH.
So the length(EF)=(AB+2$\times$1.25) m =(7.5+2.5) m =10m
And the width(FG)=(BC+2$\times$1.25) m=(5+2.5) m =7.5m
Therefore, the area of EFGH= $EF\times FG$=$10\times 7.5\ m^{2}$=75 $m^{2}$
Therefore, the area of verandah=(area of EFGH) - (area of ABCD)
=$75\ m^{2}-37.5\ m^{2}$
=$37.5\ m^{2}$
Now we are going to find the cost of cementing the verandah,
Here it is given, the cost of cementing the floor of the verandah at the rate of Rs.15 per $m^{2}$.
So we can write this as,
1 $m^{2}$ cementing cost = Rs 15
$\therefore$ 37.5 $m^{2}$ cementing cost = Rs 37.5$\times$15=562.5 $m^{2}$
Therefore, the required solution,
(i) The area of the verandah $37.5\ m^{2}$
(ii) The cost of cementing the floor of the verandah at the rate of Rs.15 per $m^{2}$ is 562.5 $m^{2}$.


Note: While calculating the length and breath of verandah we added 2 times the width of verandah with the length and breath of the floor because when you construct a verandah of fixed width then in each and every side the length is increases, therefore, the length of the floor increased form the right side and as well as left side, so including verandah the length of the outer rectangle (EFGH) is increased by two times the width of verandah and similarly goes for breath of the outer rectangle.