Question

A variable circle is drawn to touch the line $3x-4y=10$ and also the circle ${{x}^{2}}+{{y}^{2}}=1$ externally then the locus of its center is:
(a) Straight line
(b) Circle
(c) Pair of real, distinct straight lines
(d) parabola

Answer 1

Hint: We start solving the problem by assuming the center of the variable circle as $\left( h,k \right)$ and radius as r. We use the fact that perpendicular distance from the center of the circle to the tangent is equal to the radius of the circle to proceed through the problem. We also use the fact that the sum of the radius of two externally touching circles is equal to the distance between the centers of those circles to get the radius. Now we check $\vartriangle $ and ${{h}^{2}}-ab$ to get the locus of the center.


Complete step-by-step solution:
Given that we have a circle, which always touches the line $3x-4y=10$ and also the circle ${{x}^{2}}+{{y}^{2}}=1$ externally. We need to find the locus of its center.
So, we have the line $3x-4y-10=0$ as a tangent for the variable circle.
Let us assume the center of the variable circle be $\left( h,k \right)$ and the radius be r. Let us draw the given information.

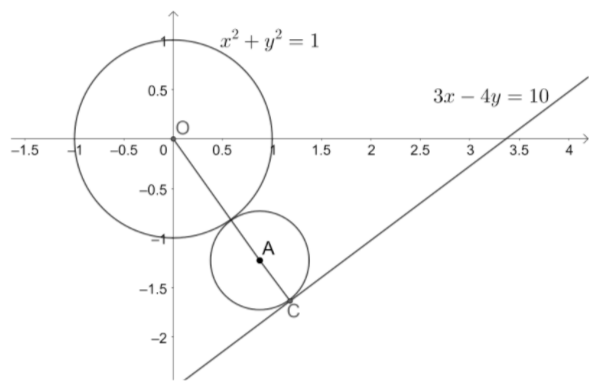
We know that the perpendicular distance from the center of the circle to the tangent is equal to the radius of the circle.
We know that the perpendicular distance from a point $\left( {{x}_{1}},{{y}_{1}} \right)$ to the line $px+qy+r=0$ is $\dfrac{\left| p{{x}_{1}}+q{{y}_{1}}+r \right|}{\sqrt{{{p}^{2}}+{{q}^{2}}}}$.
So, we have got perpendicular distance OD = radius of the variable circle.
We have got $\dfrac{\left| 3h-4k-10 \right|}{\sqrt{{{3}^{2}}+{{4}^{2}}}}=r$ .
We have got $\dfrac{\left| 3h-4k-10 \right|}{\sqrt{9+16}}=r$.
We have got $\dfrac{\left| 3h-4k-10 \right|}{\sqrt{25}}=r$.
We have got $\dfrac{\left| 3h-4k-10 \right|}{5}=r$---(1).
We know the sum of the radius of two externally touching circles is equal to the distance between the centers of those circles.
We have got OA = R + r. Where R is the radius of ${{x}^{2}}+{{y}^{2}}=1$.
We know that center and radius of circle ${{x}^{2}}+{{y}^{2}}={{s}^{2}}$ is $\left( 0,0 \right)$ and s. So, the center and radius of circle ${{x}^{2}}+{{y}^{2}}=1$ is $\left( 0,0 \right)$ and 1.
We know that the distance between two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$.
So, we have got $\sqrt{{{\left( h-0 \right)}^{2}}+{{\left( k-0 \right)}^{2}}}=1+r$.
From equation (1),
We have got $\sqrt{{{h}^{2}}+{{k}^{2}}}=1+\dfrac{\left| 3h-4k-10 \right|}{5}$.
Squaring on both sides we get
We have got ${{\left( \sqrt{{{h}^{2}}+{{k}^{2}}} \right)}^{2}}={{\left( 1+\dfrac{3h-4k-10}{5} \right)}^{2}}$.
We have got ${{h}^{2}}+{{k}^{2}}={{\left( \dfrac{5+3h-4k-10}{5} \right)}^{2}}$.
We have got ${{h}^{2}}+{{k}^{2}}=\dfrac{{{\left( 3h-4k-5 \right)}^{2}}}{25}$.
We have got $25{{h}^{2}}+25{{k}^{2}}=9{{h}^{2}}+16{{k}^{2}}+25-24hk-30h+40k$.
We have got $16{{h}^{2}}+9{{k}^{2}}+24hk+30h-40k-25=0$.
Let us substitute $\left( x,y \right)$ in place of $\left( h,k \right)$ to get the generalized locus.
We get locus as $16{{x}^{2}}+9{{y}^{2}}+24xy+30x-40y-25=0$.
∴ The locus is $16{{x}^{2}}+9{{y}^{2}}+24xy+30x-40y-25=0$.
We know that $\vartriangle $ for $a{{x}^{2}}+b{{y}^{2}}+2hxy+2gx+2fy+c=0$ is $abc+2fgh-a{{f}^{2}}-b{{g}^{2}}-c{{h}^{2}}$.
Let us find $\vartriangle $ for $16{{x}^{2}}+9{{y}^{2}}+24xy+30x-40y-25=0$.
So, we have got $\vartriangle =\left( 16\times 9\times -25 \right)+\left( 2\times 12\times 15\times -20 \right)-\left( 16\times {{\left( -20 \right)}^{2}} \right)-\left( 9\times {{\left( 15 \right)}^{2}} \right)-\left( -25\times {{\left( 12 \right)}^{2}} \right)$.
We have got $\vartriangle =-3600-7200-\left( 16\times 400 \right)-\left( 9\times 225 \right)-\left( -25\times 144 \right)$.
We have got $\vartriangle =-3600-7200-6400-2025+3600$.
We have got $\vartriangle =-15625$.
We have got $\vartriangle \ne 0$.
Let us find the value of ${{h}^{2}}-ab$.
We have got ${{h}^{2}}-ab={{\left( 12 \right)}^{2}}-\left( 16\times 9 \right)$.
We have got ${{h}^{2}}-ab=144-144$.
We have got ${{h}^{2}}-ab=0$.
We know that for a parabola the conditions satisfied are $\vartriangle \ne 0$ and ${{h}^{2}}-ab=0$.
∴ The locus of the center of the variable circle is Parabola.
The correct option for the given problem is (d).

Note: We should not say the structure of locus without checking $\vartriangle $ and ${{h}^{2}}-ab$. We should always give locus in terms of x and y as we take the axes as x and y. There will be problems where we get the locus as an ellipse, hyperbola, etc. So, we should not say without getting the final result.