Question

A uniform thin circular ring of radius ‘R’ and mass ‘M’ is rotating about its fixed axis, passing through its center and perpendicular to its plane of rotation, with a constant angular velocity ‘$\omega$’. Two objects each of mass ‘m’ are attached gently to the opposite side of the diameter. The ring now rotates with the angular velocity of:
$\text{A}. \quad \dfrac{\omega M}{M+m}$
$\text{B}. \quad \dfrac{\omega M}{M+2m}$
$\text{C}. \quad \dfrac{\omega M}{M-2m}$
$\text{D}. \quad \dfrac{\omega (M+3m)}{M}$

Answer 1

Hint: By the principle of conservation of angular momentum, we understand that if the net external torque acting on the system is zero, then the angular momentum of the system remains the same i.e. constant. Mathematically we can say that if $\tau_{ext}= \dfrac{dL}{dt}=0$, then ‘L’ i.e. angular momentum of the system remains constant.

Formula used: $L=I\omega$.

Complete step by step answer:

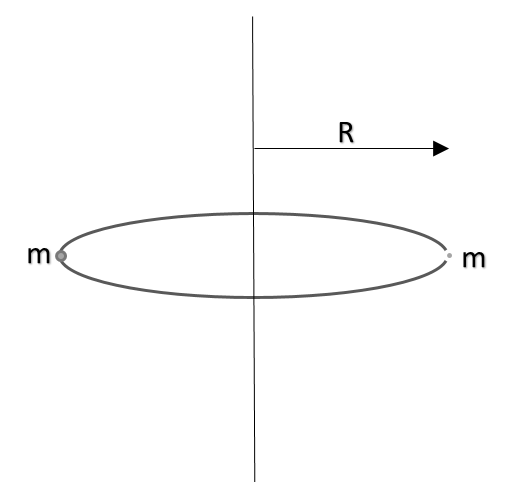
As mentioned in the question itself, the masses are placed gently, hence it means that net external torque applied on the system is zero. Hence the angular momentum of the system before and after the event shall remain the same. Hence applying:
$L=I\omega$
Let moment of inertia before the event be $I_1$ and angular velocity be $\omega_1$ and that after the event be $I_2$ and $\omega_2$, then for angular momentum being constant, we can write:
$I_1\omega_1=I_2\omega_2$
Now, for$I_1$, we know
For a uniform circular ring of radius ‘R’ and mass ‘M’, moment of inertia about an axis passing through the center of ring and perpendicular to the plane is $MR^2$
Hence $I_1=MR^2$
$\omega_1=\omega$
And finally $I_2=mR^2+mR^2+MR^2=2mR^2+MR^2$
Thus, $\omega_2 = \dfrac{I_1\omega_1}{I_2}$
Or $\omega_2=\dfrac{MR^2\omega}{2mR^2+MR^2} = \dfrac{M\omega}{2m+M}$

Hence final angular velocity will be $\dfrac{\omega M}{M+2m}$

So, the correct answer is “Option B”.

Note: Here we wrote directly that the moment of inertia of the particles as $mR^2$ considering the particle as a point mass. But in case the particle is not point mass, then we have to use the parallel axis theorem to write its moment of inertia about the required axis. Also the moment of inertia is a tensor quantity which means it has no direction but has dependency on orientation of the body.