Question

A uniform rope of length L is pulled by a force F on a smooth surface. Find tension in the rope at a distance x from the end where force is applied.

Answer 1

Hint: The tension in the rope at the specified distance will be equivalent to the amount of force that is required to move the rest of the rope with acceleration a. Use this to first find the mass of the rest of the rope and multiply it with the acceleration and you should arrive at an expression for the tension in the rope in terms of the original pulling force and the length of the rope.
Formula Used:
Force $F =ma$
Linear mass density $= \dfrac{m}{L}$

Complete step by step answer:
We are given that the length of the rope is L and it is pulled by a force F. Assuming the mass of the rope to be m, the acceleration of the rope in the direction of the pulling force can be given as:
$a =\dfrac{F}{m}$

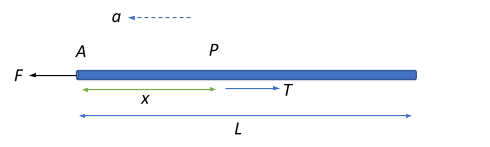
Consider a point P that is at a distance x from the end A, which is the end where the force is applied.
This pulling force creates a tension in the rope in the opposite direction which is equivalent in magnitude to the force that is required to move the rest of the rope with the same acceleration a.
The length of rest of the rope is given as $(L-x)$. Now, the mass per unit length, or the linear mass density of the rope can be given as: $\dfrac{m}{L}$. Therefore, the mass of the rest of the rope will be: $m^{\prime} = \dfrac{m}{L}(L-x)$
Therefore, the force required to move the rest of the rope while maintaining an acceleration a is given as:
$F^{\prime} = m^{\prime} \times a = \dfrac{m}{L}(L-x) \times \dfrac{F}{m} = F\dfrac{L-x}{L}$
Since this force is equivalent to the tension in the rope at a distance x from end A, the tension will thus be: $T = F\dfrac{L-x}{L}$

Note:
Remember that the linear mass density is a measure of the mass of an object per unit length of the object. This comes in handy whenever we are in need of the mass of not the whole object but a part of the length of the object. Note that this is applicable only for those objects that have a uniform density throughout their structure and do not have any variationally dense or concentrated parts.