Question

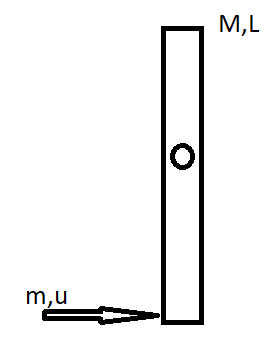
A uniform rod of mass M and length L is hinged at the centre. A particle of mass m and speed up sticks after hitting the end of the rod. What is the angular velocity of the rod just after the collision?

(A) $ \dfrac{{6mu}}{{(m + 3M)L}} $
(B) $ \dfrac{{6mu}}{{(m + 3M)L}} $
(C) $ \dfrac{{6Mu}}{{(m + 3M)L}} $
(D) $ \dfrac{{6Mu}}{{(m + 3m)L}} $

Answer 1

Hint : Understand that there is no external torque that does any work. The particle doesn’t produce any torque on the rod as such. Due to this reason angular momentum is conserved. Equate the angular momentum and find angular velocity.

Complete step by step answer
Given that there is a uniform rod of mass M and length L that is hinged at the center. Now, it is essential to understand that, when an object is hinged or fixed at the center, the only possible motion when a force applied to its ends is rotational.
Hence the velocity undergone by the rod, when the particle of mass m and velocity u striking the ends of the rod is angular. Hence, we see here that the particle doesn’t affect the angular momentum of the rod.
This means that the angular momentum of the System is conserved from the initial stage where the particle doesn’t hit and after the particle hits.
Now, let $ {L_i} $ be the initial angular momentum of the particle that strikes the rod and let $ {L_f} $ be the final angular momentum after the particle hits the rod.
Now, Angular momentum of the rod is given by the formula,
 $ {L_i} = \dfrac{{muL}}{2} $ , where m is mass of the particle, u is the velocity of the particle
Now final angular momentum is calculated using
 $ L = I \times \omega $ ,As angular momentum is product of Inertia and angular velocity of the body
Now
 $ {L_f} = {I_{particle}} \times {\omega _{particle}} + {I_{rod}} \times {\omega _{Rod}} $
Now, Moment of Inertia of a rod is $ \dfrac{{M{L^2}}}{{12}} $ and moment of inertia of ball is $ \dfrac{{m{L^2}}}{4} $
 $ {L_f} = \dfrac{{M{L^2}}}{{12}} \times \omega + \dfrac{{m{L^2}}}{4} \times \omega $ (Angular Velocity is equal since there is no initial of rod)
 $ {L_f} = \dfrac{{(M + 3m){L^2}}}{{12}} \times \omega $
Now, we know that the momentum is conserved and hence $ {L_i} $ = $ {L_f} $
 $ \dfrac{{muL}}{2} = \dfrac{{(M + 3m){L^2}}}{{12}} \times \omega $
 $ mu = \dfrac{{(M + 3m)L}}{6} \times \omega $
 $ \dfrac{{6mu}}{{(M + 3m)L}} = \omega $
Hence, Option (D) is the correct answer for the given question.

Note
Angular velocity can also be calculated as the product of linear momentum of the object and the radius of the object affected by linear momentum.