Question

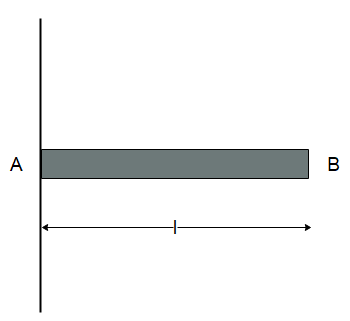
A uniform rod of length $ l $ and mass $ m $ is free to rotate in a vertical plane about A. The rod initially in a horizontal position is released. The initial angular acceleration of the rod is (Moment of inertia of the rod about A is $ \dfrac{{m{l^2}}}{3} $

A) $ \dfrac{{3g}}{{2l}} $
B) $ \dfrac{{2l}}{{3g}} $
C) $ \dfrac{{3g}}{{2{l^2}}} $
D) $ \dfrac{1}{2} $

Answer 1

Hint: We will calculate the angular acceleration of the rod using the relation of torque with the force and angular acceleration. The force responsible for the rotation of the rod will be the weight of the rod.

Formula used
In this solution, we will use the following formula:
-Toque of the rod $ \tau = I\alpha $ where $ I $ is the moment of inertia and $ \alpha $ is the angular acceleration
-Relation of force and torque: $ \tau = F.r $ where $ r $ is the distance from the axis where the force is acting

Complete step by step answer:
When the rod is released from the horizontal position, the force acting on the rod will be due to its weight i.e., $ F = mg $ .
Now the torque due to this force can be calculated as the product of the weight of the rod and distance from the rod where the weight of the rod will act. Since the mass of the rod is uniformly distributed, the weight of the rod will act on the centre of mass of the rod which lies at a distance of $ l/2 $ from the axis as
 $ \tau = F.\dfrac{l}{2} $
So, the angular acceleration will be determined from
 $ \tau = I\alpha $ as
 $ mg\dfrac{l}{2} = \dfrac{{m{l^2}}}{3}\alpha $
Hence the angular acceleration of the rod $ \alpha $ will be
$ \alpha = \dfrac{{3g}}{{2l}} $ which corresponds to option (A).

Note: While calculating the torque on the rod, we must be careful in considering the weight of the rod to act on the centre of mass of the rod and not on the edge of the rod. The acceleration we calculated is only applicable initially as afterward, the rod will move downwards and we would have to take the component of the force that acts perpendicular to the length of the rod to calculate the angular acceleration.