Question

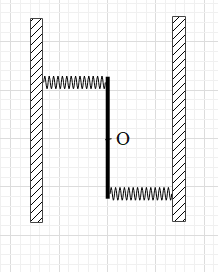
A uniform rod of length L and M is pivoted at the centre. Its two ends are attached to two springs of equal spring constants k. The springs are fixed to rigid supports as shown in the figure, and the rod is free to oscillate in a horizontal plane. The rod is gently pushed through a small angle $\theta $ in one direction and released. The frequency of oscillation is

$\text{A}\text{. }\dfrac{1}{2\pi }\sqrt{\dfrac{2k}{M}}$
$\text{B}\text{. }\dfrac{1}{2\pi }\sqrt{\dfrac{k}{M}}$
$\text{C}\text{. }\dfrac{1}{2\pi }\sqrt{\dfrac{6k}{M}}$
$\text{D}\text{. }\dfrac{1}{2\pi }\sqrt{\dfrac{24k}{M}}$

Answer 1

Hint: When the rod is rotated by an angle $\theta $, calculate the displacement of the end points of the rods using arc length formula. Then calculate the force exerted by the springs using F=kx. Then calculate the torque due to these forces. Equate this torque to $\tau =I\alpha $. Then find the angular frequency. After this, find the frequency using $f=\dfrac{\omega }{2\pi }$.

Formula used:
F=kx
$\tau =Fr$
$\tau =I\alpha $
$f=\dfrac{\omega }{2\pi }$

Complete answer:
Let us assume that there is no gravity acting on the system. Therefore, the forces acting on the rod will be the spring forces.
It is given that the rod is pivoted at point O and the two springs are attached at the end points of the rod. Then, the rod is rotated by a small angle $\theta $.
Since the angle is small, the displacement of the endpoints of the rod can be considered as linear displacement. Suppose the end points of the rod displace by a length of x.
When the rod is rotated, the end points of the rod will make arcs of radius $\dfrac{L}{2}$. The length of these arcs is x. Then, $x=\dfrac{L}{2}\theta $.
Since the angle is small, we can consider the cars as small straight line segments of length x.
Hence, we can say that the end points of the rod are displaced linearly for a length $x=\dfrac{L}{2}\theta $.
If the endpoints of the rod get displaced by x, the springs will be compressed by length x. Therefore, both the springs will push the rod by applying equal horizontal forces of magnitudes F=kx each.

These two spring forces will create a torque on the rod and the rod will undergo a simple harmonic motion.
Torque generated on the rod is $\tau =2Fr=2kx\dfrac{L}{2}$.
We know that $x=\dfrac{L}{2}\theta $.
$\Rightarrow \tau =2k\left( \dfrac{L}{2}\theta \right)\dfrac{L}{2}=k\dfrac{{{L}^{2}}}{2}\theta $.
But we also know that $\tau =I\alpha $, where I is the moment of inertia of the rod about its point of rotation and $\alpha $ is the angular acceleration of the rod.
In this case, $I=\dfrac{M{{L}^{2}}}{12}$.
$\Rightarrow \tau =\dfrac{M{{L}^{2}}}{12}\alpha $
Therefore,
$\Rightarrow \tau =k\dfrac{{{L}^{2}}}{2}\theta =\dfrac{M{{L}^{2}}}{12}\alpha $
$\Rightarrow \alpha =\dfrac{6k}{M}\theta $.
For a simple harmonic motion, $\alpha ={{\omega }^{2}}\theta $, where $\omega $ is the angular frequency of the rod.
This means that ${{\omega }^{2}}=\dfrac{6k}{M}$.
$\Rightarrow \omega =\sqrt{\dfrac{6k}{M}}$.
The frequency of the rod is given as $f=\dfrac{\omega }{2\pi }$.
Therefore, $f=\dfrac{1}{2\pi }\sqrt{\dfrac{6k}{M}}$.

So, the correct answer is “Option C”.

Note:
Note that we have taken the angle to be very small. Otherwise, the end points of the rod will not undergo simple harmonic motion.
Also note that the rod as a whole is not a simple harmonic motion. However, the different points of the rod are in simple harmonic motion.