Question

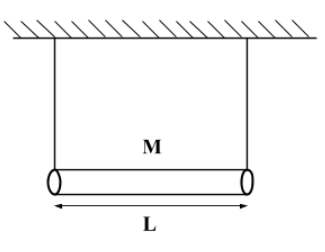
A uniform rod of length 1m and mass 2kg is suspended. Calculate tension T (in N) in the string at the instant when the right string snaps ($g=10m/s^2$).

Answer 1

Hint: To solve this problem, first find the angular acceleration. To find angular acceleration, use the equation of torque which relates mass and length with it. Then, use the formula for torque which is in terms of moment of inertia and acceleration. Equate these two equations and get the value of angular acceleration. From angular acceleration, find the acceleration by which rod falls down. Then, subtract the upward force from the downward force to get the force on the rod. Substitute the values and get the tension in the string when the right string snaps.

Complete answer:
Given: Length of the rod (l) = 1m
Mass of the rod (m) = 2kg
$g=10m/s^2$
Torque on the rod is given by,
$\tau ={\displaystyle \frac{1}{2}}mgl$ …(1)
But, torque is also given by,
$\tau =I\alpha$ …(2)
Equating equation. (1) and (2) we get,
$I\alpha ={\displaystyle \frac{1}{2}}mgl$
$\Rightarrow \alpha ={\displaystyle \frac{1}{2}}.{\displaystyle \frac{mgl}{I}}$ …(3)
We know, moment of inertia of a rod is given by
$I=13m{l}^2$
Substituting this value in the equation. (3) we get,
$\alpha ={\displaystyle \frac{1}{2}}.{\displaystyle \frac{3mgl}{m{l}^2}}$
$\Rightarrow \alpha ={\displaystyle \frac{3g}{2l}}$ …{4}
Now, the acceleration by which the center of mass falls down is given by,
$a={\displaystyle \frac{1}{2}}l\alpha$
Substituting the values from the equation. (4) we get,
$a={\displaystyle \frac{3g}{4}}$
We know,
$F=F_{down}-F_{up}$
$\Rightarrow ma=mg–T$
Substituting the values we get,
$2\times {\displaystyle \frac{3g}{4}}=2g-T$
$\Rightarrow T=2g-{\displaystyle \frac{3g}{2}}$
 $\Rightarrow T={\displaystyle \frac{g}{2}}$
Substituting the values we get,
$T=5N$

Hence, when the right string snaps, tension in the string is 5N.

Note:
Tension on the string plays an important role. Students should know that at the end where force is applied, tension is also generated at that point. Tension acts along the direction of the string. If we change the direction of the string then the direction of force also changes. An object which is not getting stretched does not have tension. We generally take the example of string and rope, but these are not the only objects that have tension. Any body or object that can experience stretching forces has tension.