Question

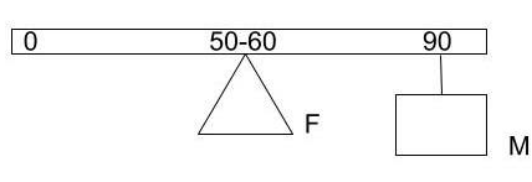
A uniform metre scale is kept in equilibrium when supported at the $60cm$ mark and a mass $M$ is suspended from the $90cm$mark in the figure. State with reasons, whether the weight of the scale is greater than, less than or equal to the weight of mass $M$.

Answer 1

Hint: Let us first get some idea about equilibrium of the rigid body. Rigid bodies are those in which, notwithstanding any external force, the spacing between particles remains constant. So, when researching rigid body equilibrium, we're primarily interested in defining the behaviour of these constituent particles under changing force or torque situations. We must examine both translational and rotational motion because we are focussing on the equilibrium of rigid things in motion.

Complete step by step solution:
Any position when the total quantity of external force or torque is zero is defined as equilibrium. This location could be anywhere near the mass centre. The linear momentum of a rigid body in translational motion is changed by an external force. In rotational motion, external torque can affect the rigid body's angular momentum.
Let us know about the moment. When the body is balanced, the total clockwise moment about a given point equals the anticlockwise moment, according to the principle of moments.
Given:
From the $$50$$ cm point, the weight of the scale W will act. According to the principle of moments
Load $\times$loadarm $=$ Effort $\times$ effortarm.
$W\times (60-50)=M\times (90-60)$
$\Rightarrow W\times 10=M\times 30$
$\Rightarrow W=3M$
So we can say that the weight of scale is three times the mass $M.$

Note:
 The linear and angular momentum of a rigid body in mechanical equilibrium remains constant over time. This means that when a body is accelerated by an external force, it does not have a linear or angular acceleration.