
A uniform cylinder of length L and M having cross-sectional area A is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half submerged in liquid of density
A.
B.
C.
D.
Answer
477.6k+ views
Hint:First, identify the forces acting on the given cylinder. Then find the magnitude and direction of each force and find the net force acting on the cylinder. Since the cylinder is in equilibrium, equate the net force to zero.
Formula used:
Complete step by step answer:
At the equilibrium position, the uniform cylinder will be standing straight up.
There will be three forces acting on the cylinder and that are the gravitational force, the spring force and the force of buoyancy exerted by the liquid.
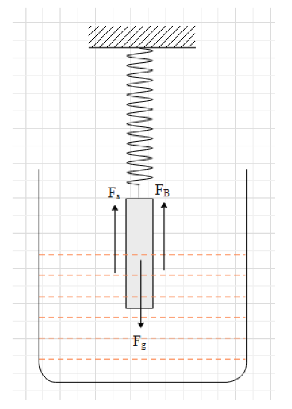
The earth exerts the gravitational force. The gravitational force on a body of mass m is given as
This means that in the case, the gravitational force on the cylinder is equal to
directed in the downward direction.
When a body is submerged in a liquid, the liquid exerts an upward force on the body called buoyant force. The magnitude of the buoyant force is given as
where
It is given that half of the cylinder is submerged in the liquid and the volume of a cylinder is equal to
This means that
The cylinder is given to be in equilibrium. Therefore, the cylinder will be at rest and the net force on it will be zero.
Let the extension in the spring be
Therefore, the net force on the cylinder is
But we know that
Take
Therefore, the correct option is A.
Note: Note that the direction of the gravitational force on a body is always in the downward direction if the body is on earth as the earth pulls down the body with the gravitational force. The direction of the buoyant force exerted by a liquid is always in the upward direction as it tries to push the body outwards.
Formula used:
Complete step by step answer:
At the equilibrium position, the uniform cylinder will be standing straight up.
There will be three forces acting on the cylinder and that are the gravitational force, the spring force and the force of buoyancy exerted by the liquid.

The earth exerts the gravitational force. The gravitational force on a body of mass m is given as
This means that in the case, the gravitational force on the cylinder is equal to
directed in the downward direction.
When a body is submerged in a liquid, the liquid exerts an upward force on the body called buoyant force. The magnitude of the buoyant force is given as
where
It is given that half of the cylinder is submerged in the liquid and the volume of a cylinder is equal to
This means that
The cylinder is given to be in equilibrium. Therefore, the cylinder will be at rest and the net force on it will be zero.
Let the extension in the spring be
Therefore, the net force on the cylinder is
But we know that
Take
Therefore, the correct option is A.
Note: Note that the direction of the gravitational force on a body is always in the downward direction if the body is on earth as the earth pulls down the body with the gravitational force. The direction of the buoyant force exerted by a liquid is always in the upward direction as it tries to push the body outwards.
Latest Vedantu courses for you
Grade 7 | CBSE | SCHOOL | English
Vedantu 7 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹45,300 per year
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

How much is 23 kg in pounds class 11 chemistry CBSE

Net gain of ATP in glycolysis a 6 b 2 c 4 d 8 class 11 biology CBSE




