Question

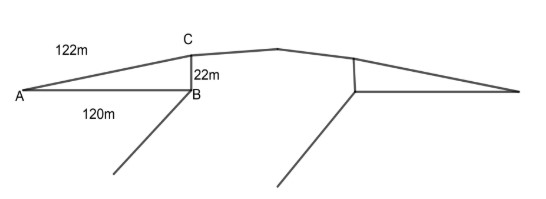
A triangular sidewalls of a flyover have been used for advertisements. The sides of the walls are 122m, 22m and 120m (see figure). The advertisements yield earning of Rs. 5000 per square meter per year. A company hired one of its walls for three months. How much rent did it pay?

Answer 1

Hint:Use the formula of area of triangle i.e. $\dfrac{1}{2}\times Base\times Height$ to find the area of the side wall. After that find the rent of one month per square meter by dividing the rate given by 12 and multiply this rent to the area to get one month rent. At the end multiply the one month rent by three to get three months rent for sidewall.

Complete step-by-step answer:
To solve the above problem we will first construct a geometrical shape from the given figure so that we can understand it conveniently.

Now, as mentioned in the problem let, $\Delta ABC$ is one of the side walls of the flyover used for the advertisement. Therefore by considering the diagram made by us we can write given accordingly,
AB = 120m
BC = 22m
AC = 122m
Amount paid for the advertisement = Rs. 5000 per square meter per year.
Time span of the advertisement = 3 Months.
As we have to find the rent paid by the company for the advertisement and we have given the rate per square meter therefore first we have to find the total area for which the amount is going t be paid,
We can easily tell from the diagram that the area of advertisement is the area of $\Delta ABC$and to find the area of triangle we should know the formula given below,
Formula:
Area of triangle $=\dfrac{1}{2}\times Base\times Height$
By using above formula and the geometry of diagram we can derive the formula of area of $\Delta ABC$ as follows,
$A\left( \Delta ABC \right)=\dfrac{1}{2}\times AB\times BC$
If we put the given values in the above equation we will get,
$\therefore A\left( \Delta ABC \right)=\dfrac{1}{2}\times 120\times 22$
$\therefore A\left( \Delta ABC \right)=120\times 11$
$\therefore A\left( \Delta ABC \right)=1320{{m}^{2}}$ …………………………… (1)
Now we have given the rent per year and we have to find the rent for three month and hence we have to find the rent for one month first,
As given in the problem,
Rent per year = Rs. 5000 per ${{m}^{2}}$
As we know that one year has 12 months therefore we can write,
Rent per 12 months = Rs. 5000 per ${{m}^{2}}$
If we divide above equation by 12 we will get the rent of one month, therefore,
Rent per month = Rs. $\left( \dfrac{5000}{12} \right)$ per ${{m}^{2}}$
$\therefore $ Rent per month per square meter = Rs. $\left( \dfrac{5000}{12} \right)$ ……………………………….. (2)
As we have found the rent of one month per square meter therefore we can find the rent of the triangular wall for one month by simply multiplying the one month’s rent by the area of $\Delta ABC$
Rent of the triangular sidewall per month = $A\left( \Delta ABC \right)\times $ Rent per month per square meter.
If we put the values of equation (1) and equation (2) in the above equation we will get,
$\therefore $ Rent of the triangular sidewall per month $=\left( \dfrac{5000}{12} \right)\times 1320$
$\therefore $ Rent of the triangular sidewall per month $=5000\times 110$
$\therefore $ Rent of the triangular sidewall per month = 550000
$\therefore $ Rent of the triangular sidewall per month = $Rs. 550000$
Now, to find the three month rent we will multiply the above equation by 3, therefore we will get,
$\therefore $ Rent of triangular side wall for three months $=550000\times 3$
$\therefore $ Rent of triangular side wall for three months = $Rs. 1650000$
Therefore the company will pay Rs. 1650000 for hiring a triangular side wall of given measurements for three months.

Note: There is a chance of silly mistakes while calculating the final rent. There are chances that you will multiply the area by 5000 without converting it into one month rent, but remember the rate given is for one year so you should convert it into one month rent.